Nächste Seite: 3.4.2 Der Backslash-Operator in Aufwärts: 3.4 Matrixfunktionen Vorherige Seite: 3.4 Matrixfunktionen Inhalt
MATLAB bietet mehrere Möglichkeiten lineare Gleichungssysteme zu lösen. Das wichtigste Lösungsverfahren ist die Gauss-Elimination oder LU-Faktorisierung. Sei
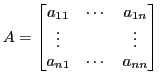
MATLAB berechnet diese Zerlegung mit sog. Spaltenpivotsuche3.1. Ist eine solche Faktorisierung berechnet, dann kann das Gleichungssystem
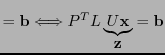 |
|||
Auch bei der Berechnung der Determinante sollte man die Gauss-Zerlegung benützen:
>> [L,U,P] = lu(A)
L =
1.0000 0 0
0.7500 1.0000 0
0.2500 1.0000 1.0000
U =
4.0000 6.0000 9.0000
0 0.5000 -2.7500
0 0 4.5000
P =
0 0 1
0 1 0
1 0 0
>> [L1,U1]=lu(A)
L1 =
0.2500 1.0000 1.0000
0.7500 1.0000 0
1.0000 0 0
U1 =
4.0000 6.0000 9.0000
0 0.5000 -2.7500
0 0 4.5000
>> P'*L - L1
ans =
0 0 0
0 0 0
0 0 0
Peter Arbenz 2008-09-24