Nächste Seite: 3.4.6 Eigenwertzerlegung Aufwärts: 3.4 Matrixfunktionen Vorherige Seite: 3.4.4 Die Methode der Inhalt
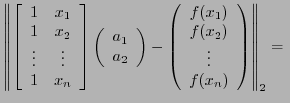 minimal
minimalVerwenden Sie die Daten:
>> n=20;
>> x = [1:n]';
>> y = x + (2*rand(size(x))-1);
Die Systemmatrix hat als erste Spalte die Stützstellen
Die Lösung des überbestimmten Gleichungssystems ist ein Vektor mit
zwei Komponenten. Werten Sie das Polynom an den Stützstellen ![]() aus, direkt oder mit polyval. Wenn Sie diese Werte in einem
Vektor Y speichern und den Befehl
aus, direkt oder mit polyval. Wenn Sie diese Werte in einem
Vektor Y speichern und den Befehl
plot(x,y,'ro',x,Y,'b')
eingeben, dann erhalten Sie (im wesentlichen) die Abbildung 3.4.