Probability foundations

In this section we will derive the formulas to compute the probabilities  which will be used in determining the most significant similarities and finally to determine whether these similarities are significant or not.

First we will abstract the problem in the following way. Suppose that we select k small intervals, each one of length $\epsilon$ in the range 0 to 1. Suppose that $\epsilon$ is small enough so that we can distribute the k intervals at random without a significant danger of overlapping them. We have now $k\epsilon$ of the interval covered and $1-k\epsilon$ uncovered. The second step consists of choosing n random points ($n \ge k$) in the unit interval. We want to determine the probability that all the kintervals receive at least one of the n random points.

Let a₁, a₂, ..., a_k, b be formal variables.

$$G_{k,n,\epsilon} = ( a_1\epsilon + a_2\epsilon + ... + a_k \epsilon + b(1-k\epsilon) )^n$$

is a generating expression  of all the events of this experiment, where a_i corresponds to an object in box i and b corresponds to an object outside all the boxes. For example, the coefficient in $G_{k,n,\epsilon}$ of a₁² b^n-2 gives the probability of two of the points falling in box 1 and all the rest falling outside all the other boxes. The coefficient of bⁿ gives the probability of all points falling outside of all the intervals.

The probability  we want to compute is the one which includes all the terms with each a_i to the power 1 or higher. These terms can be computed directly by computing which are the coefficients independent of a_i (a_i to the power 0) and subtracting this from the original $G_{k,n,\epsilon}$. To compute the probability, all the a_i and b can be set to 1. For example,

$$G_{2,n,\epsilon} = (a_1\epsilon + a_2\epsilon + b(1-2\epsilon))^n$$

The coefficient in a₁ to the power 0 is just equivalent to substituting a₁ = 0. So the component of $G_{2,n,\epsilon}$ which has at least a linear factor in a₁ is

$$G_{2,n,\epsilon}^* = (a_1\epsilon + a_2\epsilon + b(1-2\epsilon))^n - (a_2\epsilon + b(1-2\epsilon))^n$$

Repeating the same for a₂ in $G_{2,n,\epsilon}^*$ we find

$$G_{2,n,\epsilon}^{**} = (a_1\epsilon + a_2\epsilon + b(1-2\ep... ...ilon))^n - (a_1\epsilon+b(1-2\epsilon))^n + (b(1-2\epsilon))^n$$

Substituting a₁ = a₂ = b = 1and simplifying we obtain

$$P_{2,n,\epsilon} = 1 - 2(1-\epsilon)^n + (1-2\epsilon)^n$$

$P_{2,n,\epsilon}$ is the probability that when selecting n points both intervals of length $\epsilon$ include at least one point each. A more general analysis will show that

$$\begin{array}{rcl} P_{k,n,\epsilon} & = & {\displaystyle 1 - ... ...le \sum_{i=0}^k {k\choose i} (1- i \epsilon)^n} \\ \end{array}$$

Although exact, this formula is extremely ill conditioned  for computing these probabilities when $\epsilon$ is very small and n and k are relatively large. This cannot be ignored. Assuming that $n\epsilon$ remains of moderate size (neither too large nor too small), the following asymptotic approximation  can be used

$$P_{k,n,\epsilon} = (1-e^{-n\epsilon})^k (1+ \frac{kn\epsilon(... ...\epsilon}-k)}{2(e^{n\epsilon}-1)^2} \epsilon + O(\epsilon^2) )$$

For all practical purposes the most significant term, $(1-e^{-n\epsilon})^k$, is an excellent approximation for the probability.

If we have k weights from a sampled protein and we match them against an unrelated digested protein which splits into n fragments, we can view the weights of these n fragments as random.

For example, suppose that we are given k=3weights of fragments: w₁=441, w₂=893 and w₃=1415 found by mass spectrometry from an unknown protein. Suppose that the theoretical digestion of a protein in the database would give the weights v₁=410, v₂=892, v₃=925, v₄=1218 and v₅=1421. If we require an exact match, none of the values will match. If we accept a tolerance radius r=1, then v₂ is within the range of w₂, $\vert w_2-v_2\vert = \vert 893-892\vert \le 1$. If we increase the tolerance to radius r=6, then two weights will be within range, $\vert w_2-v_2\vert \le 6$and $\vert w_3-v_5\vert \le 6$. Finally we need to increase the tolerance to radius r=31 to include all the given weights in ranges. This information can be summarized by a table

$$\begin{array}{ccc} n & k & r \\ 5 & 0 & 0 \\ 5 & 1 & 1 \\ 5 & 2 & 6 \\ 5 & 3 & 31 \\ \end{array}$$

If the weights v_i were from a totally unrelated protein, they could be viewed as random values in the given range. Lets assume, for the above example, that the weights were selected in the range 400 to 1500. We can now establish an equivalence between this example and the previously computed probabilities for each of the entries in the table. For example, the second line corresponds to hitting one interval with radius 1 out of 5 random choices. The third line corresponds to hitting two intervals each one within radius 6 out of 5 random points.

Before we compute these probabilities with the above formulas, we need to consider the nature of error in molecular weights.  These errors are not of an absolute magnitude,  rather they are relative to the mass we are measuring.  I.e. an error of 1 for a mass of 1000 is equivalent to an error of 10 for a mass of 10000. Since our probability was derived on the assumption that all the intervals were of the same length, it is easiest to apply a transformation to the masses, such that a constant relative error becomes a constant absolute error. In terms of our example, an error of 1 for the mass of w₁, 441 would be equivalent to an error of $1415/441 \approx 3.2$ for w₃ with mass 1415. A standard transformation, when we want to linearize relative values, is to use the logarithms of the measures.  So instead of working with the weights, we will work with the logarithms of the weights. A tolerance of $\epsilon$ in the logarithms is equivalent to a relative tolerance of $e^{\pm \epsilon} \approx 1 \pm \epsilon$in the relative values.

$$\vert \log w_i - \log v_j \vert \le \epsilon$$

implies that

$$1-\epsilon \approx e^{-\epsilon} \le \frac{w_i}{v_j} \le e^{\epsilon} \approx 1+\epsilon$$

or

$$\frac{\vert w_i-v_j\vert}{v_j} \le \epsilon$$

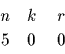
Finally, since our intervals in the theoretical derivation were based on random variables distributed in (0,1), we must make the relative errors relative to the size of the entire interval, or divide them by $\log w_{max} - \log w_{min}$ where w_max and w_min are the maximum and minimum weights that we will consider in the sample.

In our example, w_max=1500 and w_min=400 so the radius of the error for w₁, v₁ is

$$\frac{ \log 441 - \log 410} {\log 1500 - \log 400} \approx 0.055$$

the error for w₂, v₂ is

$$\frac{ \log 893 - \log 892} {\log 1500 - \log 400} \approx 0.00084$$

and for w₃, v₅ is

$$\frac{ \log 1415 - \log 1421} {\log 1500 - \log 400} \approx -0.0032$$

The above results give the minimal radius of the intervals for a hit to occur, the corresponding interval is twice this value. The following table shows the converted values and the computed probabilities

$$\begin{array}{cccc} n & k & \epsilon & P_{k,n,\epsilon} \\ 5... ... 2 & 0.0064 & 0.00080 \\ 5 & 3 & 0.11 & 0.056 \\ \end{array}$$

Surprisingly, even though w₂ is very close to v₂, the event which considers both w₂,v₂ and w₃,v₅at a greater distance, is 10 times more rare than the match of w₂,v₂ alone.

We have now all the ingredients for our algorithm. For each protein in the database we compute its digestion in, say, n fragments, and the weights of these fragments. For each searched weight w_i we find the minimum distance to one of the database weights v_jand set $d_i = 2\vert \log w_i - \log v_j\vert / ( \log w_{max} - \log w_{min})$. Now we order the distances in increasing values $d_1 \le d_2 \le d_3 \le ...$. For distance d_i, i weights are within distance d_iof database weights. For each d_i we compute P_i,n,di. The best match is considered the i for which P_i,n,diis minimal.  This probability identifies the database sequence. Finally we keep track of the m lowest probabilities (m usually between 5 and 20).

This function will be called SearchMassDb and receives as parameters a set of weights, a function which does the digestion, as shown earlier with DigestTrypsin, and the value m.

> SearchMassDb := proc( weights:array(real), Digest:procedure,
>         m:posint )
> description 'Search the database for similar mass profiles';
> if not type(DB,database) then
>     error('a protein database must be loaded with ReadDb') fi;

create the output array (with maximum probability entries)

> BestMatches := CreateArray( 1..m, [1] );

sort the input weights and compute weight bounds 

> w := sort(weights);
> lw := length(w);
> wmax := w[lw] * 1.02;
> wmin := w[1] * 0.98;
> d := CreateArray( 1..lw );
> IntLen := log(wmax) - log(wmin);

for each sequence in the database do the digestion and compute the weights 

> for e to DB[TotEntries] do
>     s := String(Sequence(Entry(e)));
>     v := Digest(s[1]);
>     v := sort(GetMolWeight(v));

compute the d_i values

>     j := 0;
>     lv := length(v);
>     for i to lw do

position j such that $v_j \le w_i \le v_{j+1}$

>         for j from j to lv-1 while v[j+1] < w[i] do od;
>         if j > 0 then
>              d[i] := 2 * abs( log(w[i])-log(v[j]) ) / IntLen
>         else d[i] := 1 fi;
>         if j < lv then
>              di := 2 * abs( log(w[i])-log(v[j+1]) ) / IntLen;
>              if d[i] > di then d[i] := di fi
>              fi;
>         od;

compute n, the number of weights between w_max and w_min

>     n := 0;
>     for j to lv do
>         if v[j] >= wmin and v[j] <= wmax then n := n+1 fi od;
>     if n < 2 then next fi;

sort the interval widths and compute the most rare event

>     d := sort(d);
>     p := 1;
>     for k to lw do
>         if d[k] > 0 then
>             pk := ( 1 - exp(-n*d[k]) ) ^ k;
>             if pk < p then kmin := k;  p := pk fi
>             fi
>         od;

Instead of working with probabilities directly, we will work with the logarithm of these probabilities.  To make these measures similar to the similarity scores of matches, we will compute $-10 \log p$. This measure will now be comparable to scores   obtained from alignments using the standard Dayhoff matrices. 

>     sim := -10 * log10(p);
>     if sim > BestMatches[1,1] then

new smallest probability found, insert and reorder BestMatches

>         BestMatches[1] := [sim,e,n,kmin];
>         BestMatches := sort( BestMatches, x -> x[1] );
>         fi
>     od;
> BestMatches
> end: