

Next: Extension to systems of
Up: Partial inverse heuristic for
Previous: Inverting functions
We have also run the random tests against several classical methods
for finding zeros.
Table 7 shows the results for Newton's method and
table 8 shows the results for the Secant method.
These are shown for comparison, and we can see that both
are successful less often and require more time.
Table 7:
Newton's method,
x-f(x)/f'(x)
| 66641 random equations |
| method |
failures |
| converged to a root |
34.36% |
converged to a non-root |
2.95% |
| failed |
65.64% |
diverged |
53.24% |
| average time |
1.595 |
outside domain |
19.94% |
| time per root |
4.644 |
too many iterations |
23.87% |
| |
|
iterator fails |
.00% |
|
Table 8:
Secant method (2-point method)
| 66641 random equations |
| method |
failures |
| converged to a root |
37.40% |
converged to a non-root |
4.46% |
| failed |
62.60% |
diverged |
72.81% |
| average time |
2.122 |
outside domain |
7.19% |
| time per root |
5.674 |
too many iterations |
15.53% |
| |
|
iterator fails |
.01% |
|
It is appropriate to run the witness examples that we proposed in
the introduction with this method.
We think the results speak for themselves.
The results for each equation are shown in tables 9,
10 and 11, where the columns are for
each iterator and the rows have the value of each iteration.
In all cases, at least one of the iteration gives the values
which were considered difficult to find.
Table 12 shows other examples, the first two taken
from [10] and the rest have been collected by the
Maple development group.
All these problems had an iterator which was successful.
Table:
Partial inverse iterators for
solving
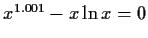
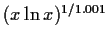 |
 |
ex0.001 |
 |
| 1.23 |
1.23 |
1.23 |
1.23 |
|
.254976... |
5.94285... |
2.71884... |
 |
|
-.348812...+.00109473...i |
3.34053... |
2.72100... |
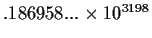 |
|
.365255...-1.09527...i |
2.77297... |
2.72101... |
 |
|
-1.31325...-.616913...i |
2.72159... |
converged |
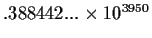 |
|
-2.14588...+3.31938...i |
2.72101... |
|
 |
|
-10.0449...-.0715578...i |
2.72101... |
|
 |
|
-23.2443...+31.2573...i |
converged |
|
 |
| diverged |
|
|
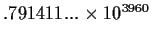 |
| |
|
|
 |
| |
|
|
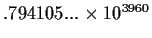 |
| |
|
|
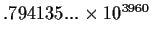 |
| |
|
|
converged |
|
Table:
Partial inverse iterators for solving

 |
 |
| 0.6 |
0.6 |
|
.632004... |
.571793... |
|
.668499... |
.546785... |
|
.710223... |
.524475... |
|
.757788... |
.504453... |
|
.811228... |
.486381... |
|
.868933... |
.469981... |
|
.925654... |
.455027... |
|
.970858... |
.441327... |
|
.994075... |
.428723... |
|
.999439... |
.417083... |
|
.999883... |
.406296... |
|
.999905... |
.396264... |
| converged |
.386907... |
| |
.378155... |
| |
.369947... |
| |
.362231... |
| |
.354961... |
| |
.348096... |
| |
.341601... |
| |
.335445... |
| |
too many iterations |
|
Table:
Partial inverse iterators for solving
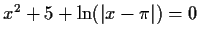
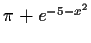 |
 |
 |
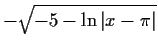 |
| 0.6 |
0.6 |
0.6 |
0.6 |
|
3.14629356... |
3.13689175... |
2.43573211...i |
-2.43573211...i |
|
3.14159299... |
3.14159230... |
2.52588218...i |
-2.52588218...i |
|
3.14159300... |
3.14159231... |
2.52864327...i |
-2.52864327...i |
| converged |
converged |
2.52872814...i |
-2.52872814...i |
| |
|
converged |
converged |
|
Table 12:
Examples from various sources,
all examples are started from x0=1.23
| equation |
| iterator |
result |
| ex-6x |
 |
converged to
2.83314... |
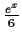 |
converged to .20448... |
| -W(-1/6) |
is
0.20448... |
 |
converged to .20448... |
 |
 |
diverged |
 |
too many iterations |
 |
too many iterations |
 |
converged to
0.83102... |
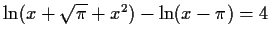 |
 |
converged to
3.45613... |
 |
converged to
50.14201... |
 |
diverged |
 |
converged to
3.45613... |
 |
diverged |
 |
converged to
50.14201... |
 |
 |
falls outside valid domain |
|
e-32 x-x -1 |
converged to
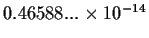 |
 |
too many iterations |
 |
converged to
3.443...+3.812...i |
|


Next: Extension to systems of
Up: Partial inverse heuristic for
Previous: Inverting functions
Gaston Gonnet
1998-07-08