


Next: Basic Definitions
Up: Examples of Enumeration Problems
Previous: Enumeration Problem: Extreme Points
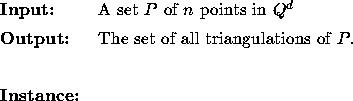
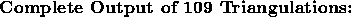
Remarks:
- (a)
- The number of output vertices might be exponential in
the size of input, while it can be very small. The upper bound
in the two dimensional case is attained
by any convex set of points and can be explicitly written as
the (n-1)st Catalan number. It is easy to construct an example
for which the number of triangulations is small (polynomial in
n and d).
- (b)
- Is there any algorithm for the triangulation enumeration enumeration problem which runs
in time polynomial in both the input size and the output size?
- (c)
- Is there such an algorithm whose space complexity is polynomial
in the size of input and the size of largest triangulation?
- (d)
- The answer to the question (b) is not known in general.
For the 2 dimensional case,
the reverse search algorithm [AF96] gives "yes"
answer to (c).
- (e)
- A closely related problem of enumerating all regular triangulations
has been studied recently. This problem appears to behave much nicely
and some efficient algorithms have been proposed. In fact, the corresponding
question (c) has been affirmatively answered by Masada.
Komei Fukuda
Wed Jun 12 17:26:21 GMT+0100 1996
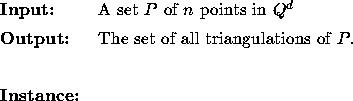
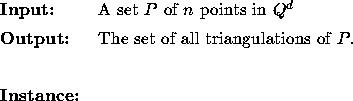
![]()