How many facets does the average polytope with $n$ vertices in $R^d$ have?

Clearly we need to define a probability distribution of points to answer the question.

Perhaps the most interesting describution for which the answer is known is the uniform distribution on the unit sphere $S^{d-1}$. The results of Buchta et al [BMT85] show that the expected number of facets is $f(d, n) = \frac{2}{d} \gamma((d-1)^2) \gamma(d-1)^{-(d-1)} (n + o(1))$ assymtotically with $n \rightarrow \infty$. The important fact is that it depends linearly on $n$ essentially. Here the function $\gamma(p)$ is defined recursively by

$$\gamma(0) =\frac{1}{2}$$

$$\gamma(p) =\frac{1}{2 \; \pi \; p \; \gamma(p-1)}.$$

Just to see how large the slope $g(d)=\frac{2}{d} \gamma((d-1)^2) \gamma(d-1)^{-(d-1)}$ of this ``linear'' function in $n$ is, we calculate it for $d \le 15$:

$d$	$g(d)$
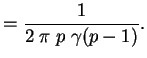2	1
3	2
4	6.76773
5	31.7778
6	186.738
7	1296.45
8	10261.8
9	90424.6
10	872190.
11	9.09402E+06
12	1.01518E+08
13	1.20414E+09
14	1.50832E+10
15	1.98520E+11