What is Voronoi diagram in
See also 3.3.
Given a set ![]() of
of ![]() distinct points in
distinct points in ![]() ,
Voronoi diagram is the partition of
,
Voronoi diagram is the partition of ![]() into
into ![]() polyhedral regions
polyhedral regions
![]() (
(![]() ). Each region
). Each region ![]() ,
called the Voronoi cell of
,
called the Voronoi cell of ![]() ,
is defined as the set of points in
,
is defined as the set of points in ![]() which are
closer to
which are
closer to ![]() than to any other points in
than to any other points in ![]() , or more precisely,
, or more precisely,
![\includegraphics[height=40mm]{vtest_fig_vo}](img154.png)
The set of all Voronoi cells and their faces forms a cell complex.
The vertices of this complex are called the Voronoi vertices,
and the extreme rays (i.e. unbounded edges) are the Voronoi rays.
For each point ![]() , the nearest neighbor set
, the nearest neighbor set
![]() of
of ![]() in
in ![]() is the set of points
is the set of points ![]() which
are closest to
which
are closest to ![]() in Euclidean distance.
Alternatively, one can define a point
in Euclidean distance.
Alternatively, one can define a point ![]() to be a Voronoi vertex of
to be a Voronoi vertex of ![]() if
if ![]() is maximal over all nearest neighbor sets.
is maximal over all nearest neighbor sets.
In order to compute the Voronoi diagram, the following construction
is very important. For each point ![]() in
in ![]() , consider
the hyperplane tangent to the paraboloid in
, consider
the hyperplane tangent to the paraboloid in ![]() at
at ![]() :
:
![]() . This hyperplane is
represented by
. This hyperplane is
represented by ![]() :
:
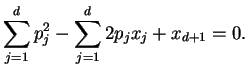
![\includegraphics[height=40mm]{vtest_fig_vo3d}](img165.png)