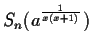 cannot be computed.
cannot be computed.
For this reason it is important to find out if Sn(a) is a
primitive root or not.
This can be done with an efficient test.
For every prime factor k of ![]() , we test whether
, we test whether
![]() .
If it is 1, then Sn(a) is a kth power, and it will
be a generator of at most
.
If it is 1, then Sn(a) is a kth power, and it will
be a generator of at most ![]() values.
By trying all the primes factors of
values.
By trying all the primes factors of ![]() we can find
the maximum k for which
we can find
the maximum k for which
![]() .
If
.
If ![]() signatures of the exponents should be computed
(mod
signatures of the exponents should be computed
(mod
![]() ).
This is not only more efficient, but could remove unwanted factors
from
).
This is not only more efficient, but could remove unwanted factors
from ![]() which may otherwise prevent signature computation.
which may otherwise prevent signature computation.