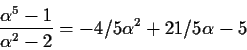Next: Exponentials, ex
Up: Algebraic numbers
Previous: Algebraic numbers
The probability of a random polynomial (mod n)
of degree k having i roots is
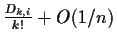 .
Dk,i are called the rencontre numbers.
Dk,1/k! is the limiting value when n grows of the
number of polynomials which will have a single root, and hence
suitable for computing signatures.
A description of these numbers can be found in
[2] pp. 65.
The exponential generating function for them is
.
Dk,i are called the rencontre numbers.
Dk,1/k! is the limiting value when n grows of the
number of polynomials which will have a single root, and hence
suitable for computing signatures.
A description of these numbers can be found in
[2] pp. 65.
The exponential generating function for them is
The limiting value, when the degree of the polynomial grows,
is
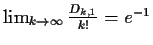 .
In other words, for random polynomials of high degree and
for large size fields, 36.79% of the time these polynomials
will have a single root suitable for use as a signature.
.
In other words, for random polynomials of high degree and
for large size fields, 36.79% of the time these polynomials
will have a single root suitable for use as a signature.
If we have more than one linear factor for all the values
of n that we are prepared to try (notice that for
polynomials of degree 2 we either have two linear factors
or none), then we have multiple choices.
Whenever we have multiple choices we have to compute all
signatures arising from them.
So if we have a square root and an algebraic number which
factors in no less than 3 linear terms we will have to
compute
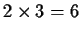 signatures.
signatures.
If all the signatures are
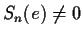 the expression
is not zero.
If all Sn(e)=0 then the expression is identically
zero with some probability of error.
Else we cannot decide and the procedure fails.
the expression
is not zero.
If all Sn(e)=0 then the expression is identically
zero with some probability of error.
Else we cannot decide and the procedure fails.
Example.
Let 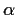 and p(x) be defined as before.
The following is a standard normalization of
a rational expression containing algebraic numbers:
and p(x) be defined as before.
The following is a standard normalization of
a rational expression containing algebraic numbers:
To compute the signature of these expressions, we need to
find an n for which p(x) factors with only one linear
factor.
n=5 will fail to compute some fractions on the right
hand side.
For n=7, p(x) does not factor.
For n=11,
has a single linear factor and we decide to use it.
So we set
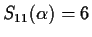 and
and
as expected.



Next: Exponentials, ex
Up: Algebraic numbers
Previous: Algebraic numbers
Gaston Gonnet
1999-07-04
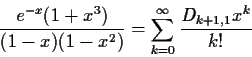
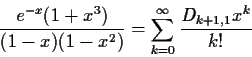
![]() signatures.
signatures.
![]() the expression
is not zero.
If all Sn(e)=0 then the expression is identically
zero with some probability of error.
Else we cannot decide and the procedure fails.
the expression
is not zero.
If all Sn(e)=0 then the expression is identically
zero with some probability of error.
Else we cannot decide and the procedure fails.
![]() and p(x) be defined as before.
The following is a standard normalization of
a rational expression containing algebraic numbers:
and p(x) be defined as before.
The following is a standard normalization of
a rational expression containing algebraic numbers: