Exponentials of complex numbers pose a more immediate problem.
We have seen that to represent i, n has to be either of the
form 4k+1 or 8k+2.
In both cases, ![]() is a multiple of 4 and it is not
possible to represent
is a multiple of 4 and it is not
possible to represent
![]() .
Since
.
Since ![]() requires i to be represented in the base and in the
exponent, we need to resolve this problem if want to compute
signatures of trigonometric functions.
requires i to be represented in the base and in the
exponent, we need to resolve this problem if want to compute
signatures of trigonometric functions.
To represent i and the square root of other non-residues we
will use one field extension.
We will call this extension ![]() , and since it has no
representation (mod n) we will have to operate with it in
symbolic form.
Without loss of generality, we will assume that it satisfies
, and since it has no
representation (mod n) we will have to operate with it in
symbolic form.
Without loss of generality, we will assume that it satisfies
![]() .
So when this is needed, our signatures will be of the form
.
So when this is needed, our signatures will be of the form
![]() and called
and called ![]() -forms.
(It is easy to see that the signatures of the square roots
of non-residues are of the form
-forms.
(It is easy to see that the signatures of the square roots
of non-residues are of the form ![]() , so as a side effect
we can represent the square roots of all the integers.)
Arithmetic is done as with polynomials in
, so as a side effect
we can represent the square roots of all the integers.)
Arithmetic is done as with polynomials in ![]() and
every time that we generate
and
every time that we generate ![]() we substitute it for -1.
Inverses and divisions are done by multiplying the numerator and
denominator by the conjugate with respect to
we substitute it for -1.
Inverses and divisions are done by multiplying the numerator and
denominator by the conjugate with respect to ![]() .
The only problem to resolve is how to compute exponentials of
.
The only problem to resolve is how to compute exponentials of
![]() -forms, and here is where we will introduce signatures
of trigonometrics.
-forms, and here is where we will introduce signatures
of trigonometrics.
Let
![]() , where r and
, where r and ![]() are relatively
prime, neither r nor
are relatively
prime, neither r nor
![]() are small
and r is otherwise randomly chosen.
With such an r, T is also a primitive root (mod n).
Since neither r nor 1/r are small, there is little chance, O(1/n),
of polynomials in S(e)x being confused with polynomials in Tx.
In what follows, n will be chosen so that i can be represented.
The signatures of the trigonometric functions will be
computed as follows.
are small
and r is otherwise randomly chosen.
With such an r, T is also a primitive root (mod n).
Since neither r nor 1/r are small, there is little chance, O(1/n),
of polynomials in S(e)x being confused with polynomials in Tx.
In what follows, n will be chosen so that i can be represented.
The signatures of the trigonometric functions will be
computed as follows.

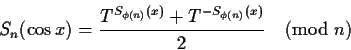
It is not difficult to verify that with these definitions,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , etc.
, etc.