


Next: Signature of
Up: Open problems with signatures
Previous: Signatures of boolean expressions
We do not know how to compute the signature of  within arguments of trigonometrics.
within arguments of trigonometrics.
 plays a very specific role in trigonometric functions.
So far all attempts to find
plays a very specific role in trigonometric functions.
So far all attempts to find  so that the trigonometric
functions compute correctly yield values which make too many
mistakes.
The reason for the apparent failures to find a signature are
illustrated in the following.
Since
so that the trigonometric
functions compute correctly yield values which make too many
mistakes.
The reason for the apparent failures to find a signature are
illustrated in the following.
Since
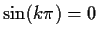 for integer k and
for integer k and
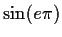 is reduced to
is reduced to
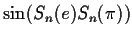 and
all signatures are integers, the signature of sin of any expression
times
and
all signatures are integers, the signature of sin of any expression
times  becomes 0.
In other words, the condition k is an integer is not unique
when we are dealing with signatures, all expressions are mapped
to integers.
New ideas are needed to resolve this problem.
becomes 0.
In other words, the condition k is an integer is not unique
when we are dealing with signatures, all expressions are mapped
to integers.
New ideas are needed to resolve this problem.
Gaston Gonnet
1999-07-04