


Next: The Pairwise Comparison of
Up: Insertions and Deletions
Previous: Insertions and Deletions
Gap Probabilities and Penalties
Our algorithms for aligning amino acid sequences are based on the
test of whether the two sequences evolved from a common ancestral
sequence or not.
This model allowed us to derive scores (used by the dynamic
programming algorithm) from the mutation probabilities.
In this section, we derive gap penalty
costs from the probabilities of a gap occuring.
The gap model
we use here is the one which is implicit
in the vast majority of the present literature. This
assumes that gaps are accidents at the DNA level which
produce a random insertion or deletion of k amino acids
with probability q(k).
This probability is independent of the amino acids being
inserted or deleted and of any neighbouring amino acids.
It is a natural assumption that this probability also
depends on the PAM distance t between the two sequences,
in particular, gaps in similar sequences are less frequent than gaps
in distant ones.
Then
Gap penalties used with dynamic programming are typically
of the form a+bk.
In some cases the values of a and b depend on the PAM
distance t.
This gap penalty function used for dynamic programming will
be denoted by d(k,t).
For example
d(k,t) = a+bk
The linear gap penalty
function is very popular, in part
because it is possible to compute dynamic programming
alignments very efficiently using Gotoh's algorithm[18].
The relation between d(k,t) and q(k,t) is simply
This relation is not well known, so we will prove it here.
Readers not interested in the mathematical theory of
alignments should skip the rest of this section.
The purpose of aligning sequences with dynamic programming
is to find the alignment which maximizes the probability
of the two sequences having evolved
from a common ancestor
as opposed to being just random sequences.
Let A and B be two sequences with lengths nA and
nB.
Let Ai be the ith amino acid in A (similarly
for B).
Let fi be the frequency of amino acid i as defined in the
previous section.
The probability that the two sequences are random is
For example, given an alignment
where X denotes the unknown ancestral parent sequence.
The probability of this alignment being the consequence
of having a common ancestor is
for all the possible X1 which evolved into A1 on one
side and into B1 on the other, and similarly for X2
where this term denotes the probability of a gap of length
3 on one sequence times the probability of the sequence
B3B4B5 on the other and
for the alignment of A3 against B6.
For this alignment the quotient of the probabilities is
once property grouped and simplified.
To find the alignment which maximizes this probability
we transform the maximization of a product
(of all positive
values) into the maximization of a sum by computing the
logarithm of each term.
To find the alignment which maximizes a sum, we use the
dynamic programming algorithm.
For historical reasons and to work with simpler numbers,
these logarithms are multiplied by 10, which has no effect
on the maximization process.
Notice that the terms like
are exactly the values of the standard Dayhoff matrices.
The deletion cost for the above example, under dynamic
programming, must be
It is obvious how to generalize this result for any number
or length of gaps.
The relationship can be applied in two directions:
either we can estimate the probabilities from a sample and
compute the appropriate gap penalties or we can compute
the probabilities that are implied by a gap penalty
function.
A linear gap penalty function implies an exponential
distribution of probabilities.
implies
q(k,t) = 10a/10 (10b/10)k
For example, if a=-10 and b=-3, then
This further implies that the probability of a gap, of any
length, is
in our example, the probability of having a gap would be
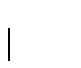 .
Finally, the expected length of a gap is
.
Finally, the expected length of a gap is
in our example, the expected length of a gap would be
2.0011.



Next: The Pairwise Comparison of
Up: Insertions and Deletions
Previous: Insertions and Deletions
Gaston Gonnet
1998-09-15
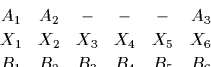
![\begin{displaymath}D[A_1,B_1] = 10 \log_{10} ( \frac{(M^t)_{B_1A_1}}{f_{B_1}} ) \end{displaymath}](img119.gif)
 .
Finally, the expected length of a gap is
.
Finally, the expected length of a gap is