


Next: Bibliography
Up: Using Traveling Salesman Problem
Previous: Examples
We have introduced a new tree construction method that constructs
the tree with the minimum score for a given set of
sequences. By using a Traveling Salesman approach to find a
circular tour and the sequence data, we can construct the the tree
with the minimum score in
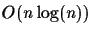 time. We can
guarantee that the reconstructed tree is correct, if the error of
the distance measurement does not exceed
time. We can
guarantee that the reconstructed tree is correct, if the error of
the distance measurement does not exceed
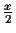 ,
where x
is the shortest edge. The probability to get a wrong circular
order is very low, as all other correct circular orders have to
be worse than the wrong order. If the errors of the distance
measurements are very large, then better results can be achieved
via dynamic programming. But we think it still is important to use
different tree construction algorithms and to compare the results
and decide in each case which tree is suited best.
,
where x
is the shortest edge. The probability to get a wrong circular
order is very low, as all other correct circular orders have to
be worse than the wrong order. If the errors of the distance
measurements are very large, then better results can be achieved
via dynamic programming. But we think it still is important to use
different tree construction algorithms and to compare the results
and decide in each case which tree is suited best.
Chantal Korostensky
1999-07-14