


Next: About this document ...
Up: Appendix
Previous: Search Space and Error
The dynamic programming version of our algorithm is very simple:
instead of connecting the two leaves with the smallest error
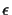 ,
the best k connections are chosen (where k is a
user specified parameter). At the end, the tree with the overall
smallest error
,
the best k connections are chosen (where k is a
user specified parameter). At the end, the tree with the overall
smallest error
 is chosen. If the number of trees at
the end is t, then the probability get an edge x wrong is much
lower: in order to get a wrong connection, all k connections
have to be wrong:
is chosen. If the number of trees at
the end is t, then the probability get an edge x wrong is much
lower: in order to get a wrong connection, all k connections
have to be wrong:
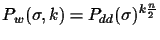 in the best
case, and
in the best
case, and
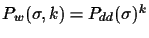 in the worst case.
in the worst case.
To show the difference we build the same table again, for
k=3:
Figure:
Probability to get the shortest edge x
wrong depending on the standard deviation  of the error
of the error
 of the distance measurements in terms of x with
dynamic programming (k=3).
of the distance measurements in terms of x with
dynamic programming (k=3).
 |
If we would simply keep all k trees at each step, the number of
resulting would grow exponentially. In the worst case, we would
get 2n-3 trees, as this is the number of possible different
trees that can be built given a circular order. Note that this can
only happen in the worst case, if the tree is completely
unbalanced (if the tree depth is almost n).
In real cases, many trees will end up being the same during the
construction process. I.e. if we first connect leaves 1, 2 and
then 3, 4 or first 3, 4 and then 1, 2 does not matter. The
number of different trees at the end is seldom more than 100
when performing experiments.
To identify equal trees during the dynamic programming
construction process, a unique number is created for each tree.
The number is added to a hash table. Any new tree is compared to
the hash table and only kept if it is not already in the list.



Next: About this document ...
Up: Appendix
Previous: Search Space and Error
Chantal Korostensky
1999-07-14

