

Next: Multiple sequence alignment.
Up: Definitions
Previous: Dayhoff matrices.
Aligning sequences is the process of associating some positions
of each sequence with a position of the other sequence.
This association preserves the order of the sequences.
E.g.
VNRLQQNIVSL____________EVDHKVANYKPQVEPFGHGPIFMATALVPGLYLGVPWF
VNRLQQSIVSLRDAFNDGTKLLEELDHRVLNYKPQANPFGNGPIFMVTAIVPGLHLGAPWF
Unassociated positions are called insertions (or their
counterpart deletions).
Aligning protein sequences by dynamic programming (DP) using Dayhoff
matrices is equivalent to finding the alignment which maximizes
the probability that the two sequences evolved from an ancestral
sequence as opposed to being random sequences.
More precisely, we are comparing two events
- a)
- that the two sequences are
independent of each other,
and hence an arbitrary position with amino acid
i aligned
to another arbitrary position with amino acid j has the
probability equal to the product of the individual frequencies
- b)
- that the two sequences have evolved
from some common ancestral sequence
after t units of evolution.
We use  as a shorthand for
as a shorthand for
 ,
that is
a sum over all symbols of the alphabet.
The entries of the Dayhoff matrix are the logarithm
of the quotient of these two probabilities.
,
that is
a sum over all symbols of the alphabet.
The entries of the Dayhoff matrix are the logarithm
of the quotient of these two probabilities.
Since DP maximizes the sum of the similarity measure,
DP maximizes the sum of the logarithms or
maximizes the product of these quotients of probabilities.
As a conclusion, DP finds the alignment
which maximizes the probability of having
evolved from a common ancestor (a maximum
likelihood alignment)
against the null hypothesis of being independent.
This makes aligning sequences using Dayhoff matrices a soundly
based algorithm.


Next: Multiple sequence alignment.
Up: Definitions
Previous: Dayhoff matrices.
Gaston Gonnet
1998-07-14
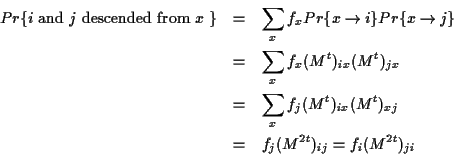
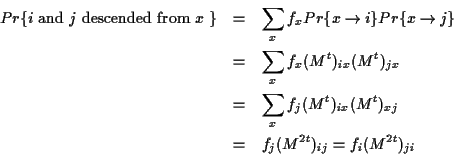
![]() as a shorthand for
as a shorthand for
![]() ,
that is
a sum over all symbols of the alphabet.
The entries of the Dayhoff matrix are the logarithm
of the quotient of these two probabilities.
,
that is
a sum over all symbols of the alphabet.
The entries of the Dayhoff matrix are the logarithm
of the quotient of these two probabilities.