Enumeration Problem: Acyclic Orientations

Remarks:

(a)

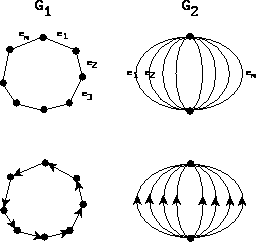
The number of output orientations might be exponential in the size of input, while it can be very small. Compare 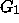and .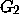

(b)

Is there any algorithm for the acyclic orientation problem which runs in time polynomial in both the input size and the output size?

(c)

Is there such an algorithm whose space complexity is polynomial in the size of input only (and independent of the output size)?

(d)

The answers to these two questions (b) and (c) are "yes." How can you design such an algorithm? Here the reverse search technique can be applied, see the cell enumeration in an arrangement of hyperplanes in [AF96].