Trigonometrics and complex arguments of exponentials

The problem of computing signatures of trigonometrics is closely related to the problem of computing exponentials of complex numbers, since if signatures are computed correctly, $S(\sin x)=S(\frac{e^{ix}-e^{-ix}}{2i})$.

Exponentials of complex numbers pose a more immediate problem. We have seen that to represent i, n has to be either of the form 4k+1 or 8k+2. In both cases, $\phi(n)$ is a multiple of 4 and it is not possible to represent $S_{\phi(n)}(i)$. Since $\sin x$ requires i to be represented in the base and in the exponent, we need to resolve this problem if want to compute signatures of trigonometric functions.

To represent i and the square root of other non-residues we will use one field extension. We will call this extension $\alpha$, and since it has no representation (mod n) we will have to operate with it in symbolic form. Without loss of generality, we will assume that it satisfies $\alpha^2+1=0$. So when this is needed, our signatures will be of the form $a+b\alpha$ and called $\alpha$-forms. (It is easy to see that the signatures of the square roots of non-residues are of the form $k\alpha$, so as a side effect we can represent the square roots of all the integers.) Arithmetic is done as with polynomials in $\alpha$ and every time that we generate $\alpha^2$ we substitute it for -1. Inverses and divisions are done by multiplying the numerator and denominator by the conjugate with respect to $\alpha$. The only problem to resolve is how to compute exponentials of $\alpha$-forms, and here is where we will introduce signatures of trigonometrics.

Let $T=S(e)^r \pmod{n}$, where r and $\phi(n)$ are relatively prime, neither r nor $1/r \pmod{\phi(n)}$ are small and r is otherwise randomly chosen. With such an r, T is also a primitive root (mod n). Since neither r nor 1/r are small, there is little chance, O(1/n), of polynomials in S(e)^x being confused with polynomials in T^x. In what follows, n will be chosen so that i can be represented. The signatures of the trigonometric functions will be computed as follows.

$$S_n(\sin x) = \frac{ T^{S_{\phi(n)}(x)} - T^{-S_{\phi(n)}(x)}} {2i} \pmod{n}$$

$$S_n(\cos x) = \frac{ T^{S_{\phi(n)}(x)} + T^{-S_{\phi(n)}(x)}} {2} \pmod{n}$$

The rules for computing exponentials and trigonometrics with $\alpha$-forms are:

$$S_n(e^{\alpha}) = T$$

$$S_n(T^{\alpha}) = 1/S_n(e) \pmod{n}$$

$$S_n(e^{a+b\alpha}) = S_n(e)^a T^b \pmod{n}$$

$$S_n(\sin (a+b\alpha)) = \frac{T^aS_n(e)^{-b}-T^{-a}S_n(e)^b}{2i} \pmod{n}$$

etc. In simpler terms, the symbol $S(e)^{\alpha}$ is assigned an arbitrary value and forced to respect the only simplification restriction which it has to follow: $(S(e)^{\alpha})^{\alpha} = S(e)^{-1}$.

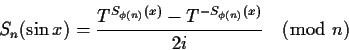
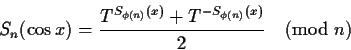
It is not difficult to verify that with these definitions, $S(\sin 0)=0$, $S(\cos 0)=1$, $S(\sin^2 x+\cos^2 x)=1$, $S(\sin (a+b))=S(\sin a \cos b + \cos a \sin b)$, etc.