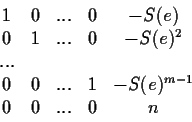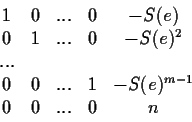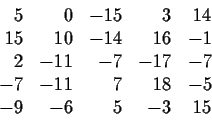Simple algebraic relations

It is important to check that these numbers, like S(e) above, do not satisfy simple algebraic relationships. It would be very unfortunate that we randomly select an S(e) which happens to be, for example, S(e)=1/3. This can be checked quite easily using the LLL lattice reduction algorithm. To do this we construct a matrix of dimension 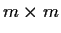$m \times m$ with the following structure:

$$\begin{array}{ccccc} 1 & 0 & ... & 0 & -S(e) \\ 0 & 1 & ... ... ... 0 & ... & 1 & -S(e)^{m-1} \\ 0 & 0 & ... & 0 & n \end{array}$$

The last row in the matrix is used to reduce the values by integer multiples of n, as should be for (mod n) computations. Every vector which is a linear combination of some of the rows, will give a polynomial in S(e) of degree at most m-1 (mod n) that is satisfied. A short vector will give a simple polynomial, hence a suspicious relationship which may be better avoided. For the above choices of S(e) and m=5, the reduced lattice is

$$\begin{array}{rrrrr} 5 & 0 & -15 & 3 & 14 \\ 15 & 10 & -14 &... ... & -11 & 7 & 18 & -5 \\ -9 & -6 & 5 & -3 & 15 \\ \end{array}$$

So the simplest polynomial relationship of degree four or less satisfied by S(e) (from the last row) is $-9S(e)-6S(e)^2+5S(e)^3-3S(e)^4+15 = 0 \pmod{n}$.

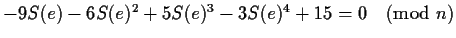Under this scheme, we can now compute the trigonometric functions with the standard complex-exponential formulas:

$$T = S(e)^{S_{n_2}(i)} \pmod{n}$$

$$S_n( \sin x ) = \frac{ T^{S_{n_2}(x)} - T^{-S_{n_2}(x)}} {2i}$$

$$S_n( \cos x ) = \frac{ T^{S_{n_2}(x)} + T^{-S_{n_2}(x)}} {2}$$

All the trigonometric relationships, including the relations with the complex exponentials will be verified. For the numerical example, S_n(i)=917163, S_n2(i)=649529 and T=2888692.