Algebraic pattern matching is defined as solving the equation
x, y, ... are called the main variables,
a, b, ... are called the parameters and
m, n, ... are called the pattern variables.
The problem is often extended to dictionaries of patterns. In this case we are searching among a set of patterns Gi and we would like to find all the ones which match a given F. In such a situation, we expect to do better than just a sequential search over each pattern.
Some examples,
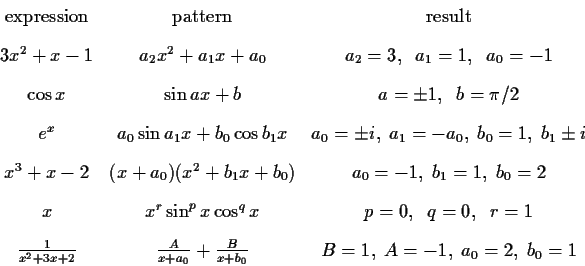
From the above examples, it is easy to see that the power of algebraic pattern matching is quite substantial and will include most of other operations, like working with complex numbers and algebraic extensions, factoring, gcds, etc.
Structural pattern matching, at the other end, attempts to match a particular form to a mathematical expression. It is like a data structure problem, or a typing problem. Often structural pattern matching does not require the definition of main variables. Only the first of the above examples would record a structural match. The following examples illustrate structural matching more precisely
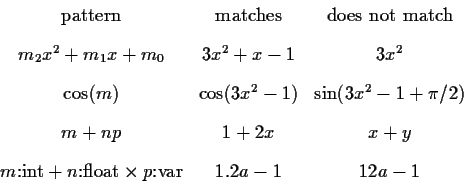
Often the pattern variables are allowed to carry typing information, as it is shown in the last line.
There are many possibilities in between these two extremes. Systems will normally implement more than just purely structural matching, often under a form that allows for the matching of missing arguments making the appropriate zero assignments.
Except for the simplest structural matching, all the matching problems are very difficult and in many cases unsolvable. For this reason, heuristic algorithms are the only hope of solving some classes of subproblems.