


Next: Field/congruence enlargement
Up: Modular mappings
Previous: Modular mappings
If a division by 0 occurs, i.e.
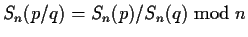 and Sn(q)=0, then we try to prove (recursively) that q is
identically zero.
If it is true, then the original expression does not make
mathematical sense.
If we have proof that the denominator is not zero, this means
that we have found an n for which
and Sn(q)=0, then we try to prove (recursively) that q is
identically zero.
If it is true, then the original expression does not make
mathematical sense.
If we have proof that the denominator is not zero, this means
that we have found an n for which
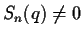 ,
and hence can continue computing the signature of the original
expression with this n.
If the division fails because
Sn(q) | n, when n is not
prime, then we can try with different values of n.
In some cases, when there are other restrictions on n,
it may not be possible to compute the division.
For example, if n is restricted to be a multiple of 2,
then the expression
,
and hence can continue computing the signature of the original
expression with this n.
If the division fails because
Sn(q) | n, when n is not
prime, then we can try with different values of n.
In some cases, when there are other restrictions on n,
it may not be possible to compute the division.
For example, if n is restricted to be a multiple of 2,
then the expression
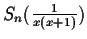 cannot be
computed.
cannot be
computed.
Gaston Gonnet
1999-07-04