Finding a circular order

Since we want to construct an evolutionary tree and therefore do not have any tree, the problem we consider is to find such an order without having any information about the tree structure. But we know that a circular order is the shortest tour through a tree [15]. To solve this problem we reduce it to the symmetric Traveling Salesman Problem (TSP): given is a matrix M that contains the 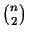$n \choose{2}$ distances of n cities [24,23]. The problem is to find the shortest tour where each city is visited once. We use a modified version of the problem: in our case, the cities correspond to the sequences and the distances are the PAM distances of the pairwise alignments. In practice, the TSP is very well studied and optimal solutions can be calculated within a few hours for up to 1000 cities and in a few seconds for up to 100 cities. There are heuristics for large scale problems that calculate near optimal solutions that are within 1% to 2% of the optimum [27,17]. For real applications we have seldom more than 100 sequences to compare simultaneously, and the calculation of the optimal TSP solution usually takes only a small fraction of the time it takes to compute all pairwise alignments to derive the PAM distances.

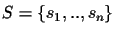
Definition 2.2   The TSP order TSP(S) of set of sequences $S = \{s_1, .., s_n\}$ is the order of the sequences that is derived from the optimal solution of a TSP, where the distances between the sequences are the pairwise PAM distances.

Definition 2.3   A tour C_i is shorter than a tour C_j (C_i < C_j) if the number of edges that are traversed by C_i is larger than the number of edges that are traversed by C_j. If C_i < C_j then the score of the tour C_i is smaller than the score of the tour C_j ( $\sum C_i < \sum C_j$).

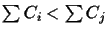
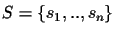
Problem 2.1 (TSP problem)   Given is a set of sequences $S = \{s_1, .., s_n\}$ and the corresponding scores of the optimal pairwise alignments. The problem is to find the shortest tour where each sequence is visited once.

Since we always talk about the same input sequences S, we will use C instead of C(S) and T instead of T(S). Let C_min be the circular tour that is derived with a TSP algorithm. Since 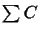$\sum C$ is the score of an evolutionary tree, 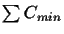$\sum C_{min}$ is the minimum score.

Lemma 2.1   C_min is a circular order of the optimal tree T_min.

Proof 2.1   Assume T_min does not have the circular order C_min(S). We know that a circular order is the shortest tour through a tree, and any other ordering leads to a longer tour. Since C_min does not belong to the set of circular orders of T_min, then the tour that results from C_min must be longer. Hence the score derived from C_min cannot be optimal, which is a contradiction.

Lemma 2.2   There exists no tree with a lower score than T_min.

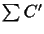
Proof 2.2   Assume this statement is wrong and there exists a tree T' with a lower score than T_min. Assume further that we know this tree T'. Hence we can derive a circular order C' easily. The sum of the PAM distances in this order ($\sum C'$) is the score of the tree. If T' really has a lower score, then the score derived from C' would have to be smaller than the score derived from C_min, which is a contradiction.

In summary, we can compute a circular order C_min without knowing T. With C_min we can compute the minimum score 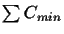$\sum C_{min}$ of the unknown tree T.