


Next: Definitions
Up: Introduction
Previous: Distance Matrix Methods
The maximum likelihood (ML) approach chooses the tree which
maximizes the probability that the observed data would have
occurred. We have a model M and the data D. The likelihood of
a tree T is the probability of the data D given the tree T
and the model M:
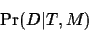 |
(2) |
When the data are fixed and the tree varies, then the values of
all
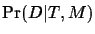 for all T need not add to one. These are
called likelihoods instead of probabilities. One candidate for the
best tree is the tree that maximizes the likelihood. The strategy
is to search over all trees, and for each topology T to find the
lengths of the edges that maximize the likelihood P(D|T). The
topology and the assignment of edge lengths that give the overall
maximum of this likelihood is the desired tree.
for all T need not add to one. These are
called likelihoods instead of probabilities. One candidate for the
best tree is the tree that maximizes the likelihood. The strategy
is to search over all trees, and for each topology T to find the
lengths of the edges that maximize the likelihood P(D|T). The
topology and the assignment of edge lengths that give the overall
maximum of this likelihood is the desired tree.
We are interested in tree construction methods that only need the
raw, unaligned sequences as input and do not require any further
information such as an MSA. In this extended abstract, we present an algorithm that runs in
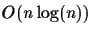 time and produces a tree with optimal score, if the
error of each distance is not greater than
time and produces a tree with optimal score, if the
error of each distance is not greater than
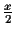 ,
where
x is the shortest edge in the tree. In the following sections we
explain our tree scoring function. We then introduce the main ideas and algorithm.
Finally, we show how the error influences the results and present
experimental results.
,
where
x is the shortest edge in the tree. In the following sections we
explain our tree scoring function. We then introduce the main ideas and algorithm.
Finally, we show how the error influences the results and present
experimental results.



Next: Definitions
Up: Introduction
Previous: Distance Matrix Methods
Chantal Korostensky
1999-07-14