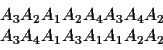Next: Bibliography
Up: Optimal Scoring Matrices for
Previous: Degrees of Freedom
We use a random matrix M as an example. For simplicity we will
assume that we have only 4 amino acids, i.e. M will be a
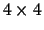 matrix. M is generated to satisfy the normal
properties: the columns should add to 1 and the pseudo-symmetry
condition
fi Mji = fj Mij must hold.
matrix. M is generated to satisfy the normal
properties: the columns should add to 1 and the pseudo-symmetry
condition
fi Mji = fj Mij must hold.
The frequency vector f can be computed from the eigenvector of
M whose eigenvalue is 1 or from the first row/column of M
[1].
The eigenvalues of M are
In this case we want to find the optimal scoring matrix for
d in the range
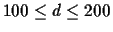 .
After setting E11=-1 and E12=1 and numerically minimizing
.
After setting E11=-1 and E12=1 and numerically minimizing
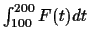 on the rest of the Eij unknowns, we obtain:
on the rest of the Eij unknowns, we obtain:
From these values, using equation 3, we can compute
S(d) = 1.258-.3307(.9786)d-1.459(.9914)d-.5098(.9830)d
The derivative of S(d) with respect to d is:
S'(d) = .007136(.9786)d+.01264(.9914)d+.008734(.9830)d
and we can see that all the terms are strictly positive,
so S(d) is strictly monotonic for all d.
Suppose we have aligned these two sequences:
The score for this alignment is
w/n = (E33+E24+E11+E23+E41+E31+E42+E22)/8 =.8076
From this value, and using any numerical method, we can find
the d* which satisfies the equation
S(d*) = .8076
The solution is
d*=149.99
The variance of the estimator is
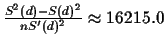 .
The variance is very large, and so is the standard
deviation (127.34), which is not unexpected for
such a short alignment.
.
The variance is very large, and so is the standard
deviation (127.34), which is not unexpected for
such a short alignment.



Next: Bibliography
Up: Optimal Scoring Matrices for
Previous: Degrees of Freedom
Chantal Korostensky
1999-07-14
![\begin{displaymath}M=\left [\begin {array}{cccc} 0.9920& 0.007612& 0.001144& 0.0...
... } 0.002821& 0.003806& 0.003051& 0.9860\end {array}
\right ]
\end{displaymath}](img49.gif)
![\begin{displaymath}M=\left [\begin {array}{cccc} 0.9920& 0.007612& 0.001144& 0.0...
... } 0.002821& 0.003806& 0.003051& 0.9860\end {array}
\right ]
\end{displaymath}](img49.gif)
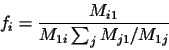
![\begin{displaymath}E =
\left [\begin {array}{cccc} - 1.0& 1.0& 3.522& 1.720
\\...
...{\medskip } 1.720& 1.331& 1.601&
- 1.596\end {array}\right ]
\end{displaymath}](img55.gif)