Scoring Pairwise Sequence Alignments

To determine if two sequences $s_1, s_2 \in \Sigma$ are related and have a common ancestor the sequences are usually aligned, and the problem is to find the alignment that maximizes the probability that the two sequences are related: To actually calculate these probabilities, one applies a Markovian model for sequence evolution [Krogh et al., 1994,Baldi et al., 1994]. This begins with an alignment of the two sequences, e.g.

    VNRLQQNIVSL____________EVDHKVANYKPQVEPFGHGPIFMATALVPGLYLLPL
    VNRLQQSIVSLRDAFNDGTKLLEELDHRVLNYKPQANPFGNGPIFMVTAIVPGLHLLPI

The gaps arise from insertions (or their counterpart deletions) during divergent evolution. The alignment is normally done by a dynamic programming (DP) algorithm using Dayhoff matrices [Gotoh, 1982,Smith and Waterman, 1981,Needleman and Wunsch, 1970,Altschul and Erickson, 1986], which finds the alignment that maximizes the probability that the two sequences evolved from an ancestral sequence as opposed to being random sequences. An affine gap cost is used according to the formula $a + l \cdot b$, where a is a fixed gap cost, l is the length of the gap and b is the incremental cost [Altschul and Erickson, 1986,Benner et al., 1993]. More precisely, we are comparing two possibilities

a)

that the two sequences arose independently of each other (implying that the alignment is entirely arbitrary, with amino acid i in one protein being aligned to amino acid j in the other is occurring no more frequently than expected by chance, which is equal to the product of the individual frequencies with which amino acids i and j occur in the database)

$$Pr \{ \mbox{$i$\space and $j$\space are independent} \} = f_i f_j$$ (1)

b)

that the two sequences have evolved from some common ancestral sequence after t units of evolution where t is measured in PAM units [Gonnet, 1994b].

$$Pr \{ \mbox{$i$\space and $j$\space descended from some $x$ } \} = \sum_x f_x Pr\{x \rightarrow i\}Pr\{x \rightarrow j\}$$ (2)

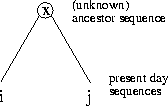
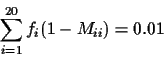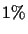
Definition 1.7   A 1-PAM unit is the amount of evolution which will change, on average, $1\%$ of the amino acids. In mathematical terms, this is expressed as a matrix M such that

$$\sum_{i=1}^{20} f_i (1 - M_{ii} ) = 0.01$$

where f_i is the frequency of the i^th amino acid.

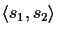
Definition 1.8   The score of an optimal pairwise alignment OPA(s₁, s₂) of two sequences s₁, s₂ is the score of an alignment with the maximum score where a probabilistic scoring method [Dayhoff et al., 1978,Gonnet et al., 1992] is used. We refer to a pairwise alignment of two sequences s₁, s₂ with $\langle s_1, s_2 \rangle$.

$$D_{ij} = 10 \log_{10} \left ( \frac { Pr \{ \mbox{$i$\space ... ... \mbox{$i$\space and $j$\space are independent} \} } \right )$$ (3)

The entries of the Dayhoff matrix are the logarithm of the quotient of these two probabilities. Note that scores represent the probabilities that the two sequences have a common ancestor. The larger the score is the more likely it is that the two sequences are homologous and therefore have a common ancestor.