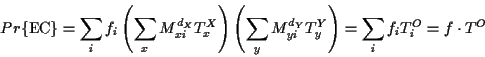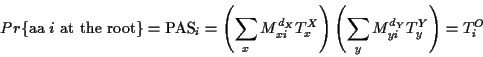

Next: Independence of the position
Up: Probability of an evolutionary
Previous: Probability of an evolutionary
Let O be the point which identifies the root of the EPT.
To compute the probability of a given position, we use the same
idea as Dayhoff et al. [6] i.e. sum over all
possible unknown amino acids o,
w, x and y and evaluate all the mutation probabilities.
The interpretation of each part of the product is simple.
For each branch between
 we will have a term
of the form
MdVv u, for each unknown internal
amino acid at node U we will have a sum for all its possibilities
(
we will have a term
of the form
MdVv u, for each unknown internal
amino acid at node U we will have a sum for all its possibilities
(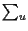 )
and for the root we have the sum of each
possible amino acid times its natural frequency of occurrence.
Lower case letters denote the particular amino acid at a given
position, e.g. x is the amino acid in a given position of sequence X.
The upper case K, R and C indicate the known amino acids at the leaves.
)
and for the root we have the sum of each
possible amino acid times its natural frequency of occurrence.
Lower case letters denote the particular amino acid at a given
position, e.g. x is the amino acid in a given position of sequence X.
The upper case K, R and C indicate the known amino acids at the leaves.
As written, this formula is very expensive to compute, it requires
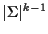 products, where k is the number of sequences.
We can reorganize this summation by the introduction of new vectors
TX and SX for each internal or external node X.
The value of the vector depends on the position of the root of the
tree and it is computed as follows
products, where k is the number of sequences.
We can reorganize this summation by the introduction of new vectors
TX and SX for each internal or external node X.
The value of the vector depends on the position of the root of the
tree and it is computed as follows
-
if X is an external leaf, i.e. a known amino acid, x
(i.e. SX is just the
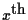 column of MdX).
column of MdX).
-
if X is an internal node, then it is a ternary node.
Let Y and Z be the adjacent nodes whose subtrees do not include
the root of the tree (away from the root).
Then
These recursive definitions can be used
if we do the computation from the leaves towards the root.
Each S corresponding to an internal node requires
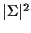 multiplications, and each T requires
multiplications, and each T requires 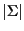 multiplications.
For k sequences, each of length m,
this requires
multiplications.
For k sequences, each of length m,
this requires
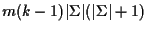 multiplications (420m(k-1) for proteins), which is
not inexpensive, but perfectly feasible.
multiplications (420m(k-1) for proteins), which is
not inexpensive, but perfectly feasible.
The computation of the probability of the EC is done with
the two immediate descendants of the root, call them X and Y.
The PAS at the root of the tree can be computed as follows:
for each amino acid at the root compute the probability of such
a configuration
where X and Y are the descendants of the root.
These are probabilities of the entire EC,
to find the relative probabilities for each amino acid
the PAS is normalized to sum 1, i.e.


Next: Independence of the position
Up: Probability of an evolutionary
Previous: Probability of an evolutionary
Gaston Gonnet
1998-07-14
![]() products, where k is the number of sequences.
We can reorganize this summation by the introduction of new vectors
TX and SX for each internal or external node X.
The value of the vector depends on the position of the root of the
tree and it is computed as follows
products, where k is the number of sequences.
We can reorganize this summation by the introduction of new vectors
TX and SX for each internal or external node X.
The value of the vector depends on the position of the root of the
tree and it is computed as follows
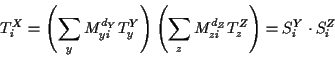
![]() multiplications, and each T requires
multiplications, and each T requires ![]() multiplications.
For k sequences, each of length m,
this requires
multiplications.
For k sequences, each of length m,
this requires
![]() multiplications (420m(k-1) for proteins), which is
not inexpensive, but perfectly feasible.
multiplications (420m(k-1) for proteins), which is
not inexpensive, but perfectly feasible.