Nächste Seite: 8.4.3 Fitting a Rectangle Aufwärts: 8.4 Fitting Lines, Rectangles Vorherige Seite: 8.4.1 Fitting two Parallel Inhalt
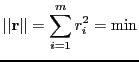
% mainorthogonal.m
Px = [1:10]'
Py = [ 0.2 1.0 2.6 3.6 4.9 5.3 6.5 7.8 8.0 9.0]'
Qx = [ 0 1 3 5 6 7]'
Qy = [12 8 6 3 3 0]'
A = [ones(size(Px)) zeros(size(Px)) Px Py
zeros(size(Qx)) ones(size(Qx)) Qy -Qx ]
[c, n] = clsq(A,2)
clf; hold on;
axis([-1 11 -1 13])
axis('equal')
plotline(Px,Py,'o',c(1),n,'-')
n2(1) =-n(2); n2(2) = n(1)
plotline(Qx,Qy,'+',c(2),n2,'-')
The Program mainorthogonal computes the two orthogonal lines