Die sogenannte ``Methode der kleinsten Quadrate''
(Least Squares) ist eine Methode, um überbestimmte lineare
Gleichungssysteme
 |
(3.4) |
zu lösen. Die 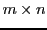 -Matrix
-Matrix 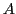 hat mehr Zeilen als
Spalten (
hat mehr Zeilen als
Spalten ( ). Wir haben also mehr Gleichungen als Unbekannte.
Deshalb gibt es im allgemeinen kein
). Wir haben also mehr Gleichungen als Unbekannte.
Deshalb gibt es im allgemeinen kein
 , das die
Gleichung (3.4) erfüllt. Die Methode der kleinsten
Quadrate bestimmt nun ein
, das die
Gleichung (3.4) erfüllt. Die Methode der kleinsten
Quadrate bestimmt nun ein
 so, dass die Gleichungen
``möglicht gut'' erfüllt werden. Dabei wird
so, dass die Gleichungen
``möglicht gut'' erfüllt werden. Dabei wird
 so
berechnet, dass der Residuenvektor
so
berechnet, dass der Residuenvektor
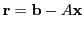 minimale Länge hat. Dieser Vektor
minimale Länge hat. Dieser Vektor
 ist Lösung der Gauss'schen Normalgleichungen
ist Lösung der Gauss'schen Normalgleichungen
(Die Lösung ist eindeutig, wenn 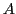 linear unabhängige Spalten hat.)
Die Gaussschen Normalgleichungen haben unter Numerikern einen
schlechten Ruf, da für die Konditionszahl
cond
linear unabhängige Spalten hat.)
Die Gaussschen Normalgleichungen haben unter Numerikern einen
schlechten Ruf, da für die Konditionszahl
cond cond
cond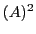 gilt und somit die Lösung
gilt und somit die Lösung
 durch die
verwendete Methode ungenauer berechnet wird, als dies durch die
Konditionszahl der Matrix
durch die
verwendete Methode ungenauer berechnet wird, als dies durch die
Konditionszahl der Matrix 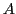 zu erwarten wäre.
zu erwarten wäre.
Deshalb wird statt der Normalgleichungen die QR-Zerlegung für
die Lösung der Gleichung (3.4) nach der Methode der kleinsten
Quadrate vorgezogen. Dabei wird die Matrix 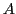 zerlegt als Produkt von
zwei Matrizen
zerlegt als Produkt von
zwei Matrizen
wobei 
 orthogonal und
orthogonal und  eine
eine 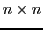 Rechtsdreiecksmatrix ist. Da orthogonale Matrizen die Länge eines
Vektors invariant lassen, gilt
Rechtsdreiecksmatrix ist. Da orthogonale Matrizen die Länge eines
Vektors invariant lassen, gilt
Daraus ist ersichtlich, dass  minimiert wird durch jenes
minimiert wird durch jenes 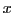 ,
welches
,
welches  löst.
löst.
In MATLAB werden überbestimmte Gleichungssysteme der Form (3.4)
automatisch mit der QR-Zerlegung gelöst, wenn man den
Backslash-Operator
x = A\b
benützt.
Peter Arbenz
2008-09-24
![]() zerlegt als Produkt von
zwei Matrizen
zerlegt als Produkt von
zwei Matrizen

