Die lineare Differentialgleichung 1. Ordnung
 |
(3.6) |
mit konstantem 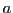 hat die Lösung
hat die Lösung
Mit der Spektralzerlegung kann dieses Resultat einfach auf Systeme von
linearen gewöhnlichen Differentialgleichungen 1. Ordnung mit konstanten
Koeffizienten
übertragen werden, welches die Lösung
hat.
Numerisch geht man so vor.
- Berechne die Spektralzerlegung von
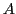 :
:
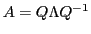 .
Die Differentialgleichung erhält dann die Form
.
Die Differentialgleichung erhält dann die Form
- Das
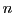 -dimensionale System zerfällt damit in
-dimensionale System zerfällt damit in 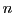 skalare
Differentialgleichungen der Form (3.6), deren Lösung
bekannt ist.
skalare
Differentialgleichungen der Form (3.6), deren Lösung
bekannt ist.
- Die Lösung des ursprünglichen Problems erhält man durch
Rücktransformation:

Peter Arbenz
2008-09-24