Collatz-Iteration. Ausgehend von einer
natürlichen Zahl  berechnet man eine Folge von
natürlichen Zahlen nach dem Gesetz
berechnet man eine Folge von
natürlichen Zahlen nach dem Gesetz
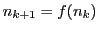 wobei
wobei
Collatz vermutete, dass diese Folge immer zum Wert 1 führt. Bewiesen
ist diese Vermutung aber nicht. Schreiben Sie eine
while-Schleife, die ausgehend von einem vorgegebenen 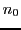 eine Collatz-Folge berechnet. Wenn Sie wollen, können alle Zahlen
bis zur Eins speichern und danach die Folge plotten [11].
Zur Bestimmung, ob eine Zahl gerade oder ungerade ist, können Sie
(wenn Sie wollen) eine der Funktionen rem oder mod
verwenden.
eine Collatz-Folge berechnet. Wenn Sie wollen, können alle Zahlen
bis zur Eins speichern und danach die Folge plotten [11].
Zur Bestimmung, ob eine Zahl gerade oder ungerade ist, können Sie
(wenn Sie wollen) eine der Funktionen rem oder mod
verwenden.
Bemerkung: Sie können sich die Aufgabe erleichtern, wenn Sie
zuerst Abschnitt 5.1 über Scriptfiles lesen.


