Consider a simple two dimensional case: ![]() ,
, ![]() and
and
![]() . In principle
the session below will work in any
. In principle
the session below will work in any ![]() and
and ![]() , although
the computation time depends heavily on the size.
, although
the computation time depends heavily on the size.
The first step is to write down the system of linear inequalities
in ![]() variables as explained in 3.2:
for each
variables as explained in 3.2:
for each ![]() ,
,
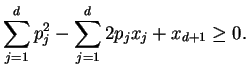
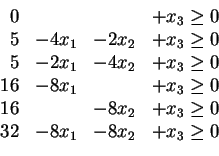
We denote by ![]() the polyhedron of all solutions
the polyhedron of all solutions ![]() satisfying the inequalities above.
Now we prepare an input file of cdd+. The file must
be in polyhedra format and for the system above,
it is rather straightforward since it essentially
codes the coefficients of the system.
satisfying the inequalities above.
Now we prepare an input file of cdd+. The file must
be in polyhedra format and for the system above,
it is rather straightforward since it essentially
codes the coefficients of the system.
* filename: vtest_vo.ine H-representation begin 6 4 integer 0 0 0 1 5 -4 -2 1 5 -2 -4 1 16 -8 0 1 16 0 -8 1 32 -8 -8 1 end incidence input_adjacency
The last two lines ``incidence'' and ``input_adjacency'' are options for cdd+. They are not necessary for listing the vertices of the polyhedron, but but can be used to generate the nearest neighbor sets and the adjacency of Voronoi cells.
Now, by running cdd+ with commands:
% cddr+ vtest.ineor
% cddf+ vtest.inewe obtain three files: vtest_vo.ext (all extreme points and rays), vtest_vo.iad (adjacency of facet inequalities) and vtest_vo.ecd (incidence of extreme points/rays and inequalities). Note that cddr+ runs in rational (exact) arithmetic and cddf+ runs in floating-point arithmetic. cddf+ runs much faster than cddr+ but it may not give a correct answer.
The file vtest_vo.ext would be something like the following:
*FINAL RESULT: *Number of Vertices =6, Rays =4 begin 10 4 rational 0 -1 0 0 1 -3/2 2 0 1 5/6 5/6 0 1 2 -3/2 0 0 0 -1 0 1 27/10 27/10 56/5 1 15/4 2 14 0 1 0 8 0 0 1 8 1 2 15/4 14 end hull
The output contains all the vertices
and extreme rays of the (unbounded) polyhedron ![]() in
in ![]() .
Namely each row starting with ``1'' represents a vertex.
So the second row
.
Namely each row starting with ``1'' represents a vertex.
So the second row
1 -3/2 2 0represents the vertex
0 -1 0 0represents the ray
By ignoring the last components, we obtain the set of six
Voronoi vertices ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() and
and ![]() and four Voronoi rays
and four Voronoi rays
![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
With the option ``incidence, cdd+ outputs vtest_vo.ecd file:
begin 10 6 7 3 : 1 5 7 3 : 1 3 5 3 : 1 2 3 3 : 1 2 4 3 : 1 4 7 3 : 2 3 6 3 : 2 4 6 3 : 4 6 7 3 : 5 6 7 3 : 3 5 6 end
Each row corresponds to the same row in vtest_vo.ine file. For example, the second data
3 : 1 3 5says the second data in vtest_vo.ine file:
1 -3/2 2 0is a voronoi vertex whose nearest neighbor set is
3 : 1 5 7indicates the ray (the first output in vtest_vo.ine file)
0 -1 0 0is determined by 1, 5 and 7th halfspaces. The 7th halfspace is an artificial one corresponding to the infinity. So this ray is determined by the input points 1 and 5 and going to infinity.
Thus, the index sets (triples, in this case) not containing
the infinity ![]() determine all Delaunay cells, and those
containing
determine all Delaunay cells, and those
containing ![]() correspond to the Voronoi rays.
correspond to the Voronoi rays.
Finally, look at the vtest_vo.iad file:
begin 7 1 5 : 2 3 4 5 7 2 4 : 1 3 4 6 3 4 : 1 2 5 6 4 4 : 1 2 6 7 5 4 : 1 3 6 7 6 5 : 2 3 4 5 7 7 4 : 1 4 5 6 end
This file contains the graph structure of the Delaunay complex and equivalently the adjacency of Voronoi cells in the Voronoi diagram.
![\includegraphics[height=40mm]{vtest_draw_vode}](img167.png)
The first line in this file:
1 5 : 2 3 4 5 7says the point
As we remarked before, this graph information can be computed much more efficiently by linear programming. See 3.5.