Dayhoff Matrices

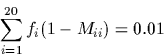
For reasons both historical and algebraic, the mutation matrix is transformed into a new matrix termed a Dayhoff matrix (in honour of the first author, Margaret O. Dayhoff). The Dayhoff matrix, D, is related to a 250-PAM mutation matrix by

$$D_{ij} = 10 \cdot log_{10} \frac{(M^{250})_{ij}}{f_i}$$

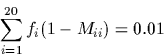
A 250-PAM distance corresponds to approximately $17\%$ identity between two sequences (see § for the proof). Many believe this distance to be at the limit of our ability to detect homology based on sequence data alone.

Aligning sequences by dynamic programming using Dayhoff matrices is equivalent to finding the alignment which maximizes the probability that the two sequences evolved from a common ancestor as opposed to being random sequences. We are comparing two events:

a)

that the two sequences are independent of each other, and hence an arbitrary position with amino acid i aligned to another arbitrary position with amino acid j has the probability equal to the product of the individual frequencies

$$Pr \{ \mbox{independent alignment of $i$\space and $j$ } \} = f_i f_j$$

b)

that the two sequences have evolved from some common ancestral sequence after some amount, t, of evolution.

$$\begin{eqnarray*}Pr \{ \mbox{$i$\space and $j$\space from a common ancestor $x$ ... ..._{ix} (M^t)_{xj} \\ & = & f_j (M^{2t})_{ij} = f_i (M^{2t})_{ji} \end{eqnarray*}$$

We use $\Sigma_{i}$ as a shorthand notation for $\Sigma_{i \in \cal{A}}$ where $\cal{A}$ is the alphabet of amino acids.

The entries of the Dayhoff matrix are ten times the logarithm of the quotient of these two probabilities.

$$D_{ij} = 10 \cdot log_{10} \left( \frac{Pr\{\mbox{$i$\space a... ...{Pr\{\mbox{$i$\space and $j$\space are independent}\}} \right)$$

(The factor of 10 is included for purely historical reasons.)

Since dynamic programming maximizes the sum of the similarity measure, dynamic programming maximizes the sum of the logarithms or the product of these quotients. Therefore, dynamic programming finds the alignment which maximizes the probabiltiy of having evolved from a common ancestor (a maximum likelihood alignment) against the null hypothesis of being independent.