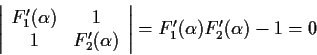Partial inverse heuristic: one theorem on convergence

ONE THEOREM ON CONVERGENCE

For functions with two occurrences of the unknown and for every root, one of the two iterators converges. Let f( x₁, x₂ ) = 0 be the equation to be solved, identifying each occurrence of x by x₁ and x₂. Let F_i(x) be the iterator derived from inverting f on x_i. Formally this means that
f( F₁(x), x ) = 0

f( x, F₂(x) ) = 0
By computing derivatives and evaluating at a root 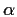$\alpha$ , we find

$f_1'(\alpha,\alpha) F_1'(\alpha) + f_2'(\alpha,\alpha) = 0$

$f_1'(\alpha,\alpha) + f_2'(\alpha,\alpha) F_2'(\alpha) = 0$

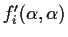For this system of equations to have a non-null solution in $f_i'(\alpha,\alpha)$ , its determinant must be zero, or
$\left \vert \begin{array}{cc} F_1'(\alpha) & 1 \\ 1 & F_2'(\... ...a) \end{array} \right \vert = F_1'(\alpha) F_2'(\alpha) -1 = 0$

$\vert F_1'(\alpha) \vert = 1 / \vert F_2'(\alpha) \vert$
So unless both absolute values are equal to one, then one iterator converges while the other diverges. This is a very encouraging result, it guarantees that one of the iterators will succeed for each of the roots.