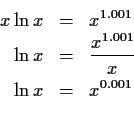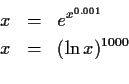Partial inverse heuristic: building additional iterators

BUILDING ADDITIONAL ITERATORS

It is easy to see that we can create an infinite number of iterators. For instance, for any iterator x = F(x)
$x = \frac{ F(x)+ax}{a+1}$
will also be fixed point iterator giving the same solution set for any 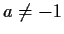$a \neq -1$ . However arbitrary iterators may not be better. Iterators with fewer occurrences of the unknown variable are generally better.
Using iterators which have the minimal number of occurrences of the unknown, guarantees to a certain degree, that we will not be generating more complicated trivial iterators.
If at any point during our isolation or after trial simplification, the resulting equation has a smaller number of occurrences of x, we will derive all possible iterators arising from this shortened equation. For example,
$\begin{eqnarray*}x \ln x & = & x^{1.001}\\ \ln x & = & \frac{x^{1.001}}{x} \\ \ln x & = & x^{0.001} \\ \end{eqnarray*}$
The grouping of powers caused a simplification and from this equation we obtain two iterators
$\begin{eqnarray*}x & = & e^{x^{0.001}} \\ x & = & ( \ln x )^{1000} \\ \end{eqnarray*}$
The first one was obtained before but the second one is new and in this case it is useful to find the largest of the roots of the original equation. This is not surprising as the new iterator has only two occurrences of the variable and falls under the previous theorem.