Partial inverse heuristic: polynomial iterators

POLYNOMIAL ITERATORS

One of the ways to create new, and hopefully better, iterators is by isolating subexpressions which are easy to invert, instead of just isolating x. For example, the equation 6x²-9x+6-ln(8+x) generates the iterators
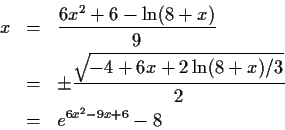
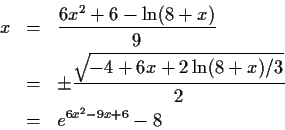
$x & = & \frac{6x^2+6-\ln (8+x)}{9} \\ & = & \pm \frac{ \sqrt{-4+6x + 2\ln (8+x)/3}}{2} \\ & = & e^{6x^2-9x+6}-8 \end{eqnarray*}$
all of which fail for the initial value x₀=1.23. For this equation we could isolate the polynomial part:

6x²-9x+6 = ln(8+x)

solve it treating the ln(8+x) as a constant, and obtain two new iterators.
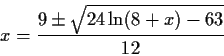
$x = \frac{ 9 \pm \sqrt{24\ln (8+x)-63 }}{12}$
Notice that these new iterators have only two occurrences of x, and hence one of them should converge for each root. The positive choice for this iterator is successful and converges very quickly to x = 0.7595... + 0.2753...i.
So we will use the following rule, each iterator which is a sum of a polynomial part and a non polynomial will be written as p(x) = F(x). Each iteration consists of evaluating F(x_i) and then solving the polynomial p(x)-F(x_i) = 0. Treating the polynomial part as a single function of x will decrease the number of occurrences of x on the rhs, and hence improve our iterators.