

Next: Conclusions
Up: Partial inverse heuristic for
Previous: Remove linear term heuristic.
To generate iterators we often need to invert functions or expressions.
For example, if at one point of our isolation process we have the
equation
x2 = h(x)
we derive
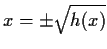 .
The choice of signs presents a problem.
The easiest way to resolve it is to derive two iterators, one
for each sign as we have done before.
Almost all functions except for lineal polynomials, present
this or other problems for isolation.
.
The choice of signs presents a problem.
The easiest way to resolve it is to derive two iterators, one
for each sign as we have done before.
Almost all functions except for lineal polynomials, present
this or other problems for isolation.
An alternative to computing inverses which are multiple-valued is
the following.
We want to compute a value xi+1 from a previous value xi.
When there are multiple choices for xi+1we want to select the one with minimal distance to xi for
convergence reasons.
I.e. select the xi+1 which makes
| xi+1-xi| minimal.
This observation is a crucial one for our algorithm.
So from
xi+12 = h(xi) we will select
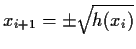 ,
the sign depending on whether
,
the sign depending on whether
 or
or
 is smaller.
This resolves the first problem, the choice between multiple
values.
For isolating, we use a function
is smaller.
This resolves the first problem, the choice between multiple
values.
For isolating, we use a function
 .
E.g. from
g(xi+1)2 = h(xi) we derive
.
E.g. from
g(xi+1)2 = h(xi) we derive
 ,
where
,
where
Inverse_square := proc( rhs, lhs )
r := sqrt( rhs );
if abs(r-lhs) <= abs(r+lhs) then r else -r fi
end;
In summary, when the result of an isolating step is a multivalued
function, we can take two approaches
- (a)
- Enumerate all iterators, either explicitly as in the case for
x2 = h(x) or as a function of an arbitrary integer n as for
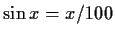 .
.
- (b)
- Leave the choice to be determined during the actual computation,
by choosing the one closest to the previous value, and hence
improving the chances of convergence.
A second problem that we have with inverting functions is a
domain problem, and it can be illustrated with the equation
from which we isolate
xi+1 = h(xi)2.
In this case there is no choice of inverse, but if h(xi) is
negative (or
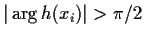 )
then the inverse cannot
be computed, as we assume that
)
then the inverse cannot
be computed, as we assume that  returns its principal
value.
E.g. for
returns its principal
value.
E.g. for
 ,
isolation gives x=1 which is not a
solution of the original equation.
Such a situation should be treated as a domain error.
In this case we use a new function to define this type of
manipulation,
,
isolation gives x=1 which is not a
solution of the original equation.
Such a situation should be treated as a domain error.
In this case we use a new function to define this type of
manipulation,
 and
and
Inverse_sqrt := proc( rhs )
a := argument( rhs );
if a <= -Pi/2 or a > Pi/2 then
ERROR( `cannot invert sqrt` )
else rhs^2 fi
end;


Next: Conclusions
Up: Partial inverse heuristic for
Previous: Remove linear term heuristic.
Gaston Gonnet
1998-07-08
![]() ,
the sign depending on whether
,
the sign depending on whether
![]() or
or
![]() is smaller.
This resolves the first problem, the choice between multiple
values.
For isolating, we use a function
is smaller.
This resolves the first problem, the choice between multiple
values.
For isolating, we use a function
![]() .
E.g. from
g(xi+1)2 = h(xi) we derive
.
E.g. from
g(xi+1)2 = h(xi) we derive
![]() ,
where
,
where