We show how to generate many fix-point iterators
of the form
xi+1 =
F(
xi)which could solve a given non-linear equation.
In particular, these iterators tend to have good global
convergence, and we show examples whereby obscure solutions
can be discovered.
Also, a systematic method for finding most or all solutions to
nonlinear equations that have multiple solutions is described.
The most successful iterators are constructed to have a small number of
occurrences of
xi in
F.
We use grouping of polynomial terms and expressions in
x,
exand
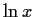
using known inverse relations to obtain better iterators.
Each iterator is tried in a limited way, in the expectation that
at least one of them will succeed.
This heuristic shows a very good behaviour in most cases,
in particular when the answer involves extreme ranges.