Convergence, divergence, random walk, invalid domains and slow convergence.

Most of the literature is concerned with the refinement phase, which in our experience is the least expensive one. The random walk phase is characterized by one or more of the following scenarios:

(a)

divergence. The values grow steadily farther from any possible solution. E.g. x e^x when tried on an $x_0 \ll -1$.

(b)

iterating outside valid domains. This may happen when the user specifies a domain for the solution, e.g. that the solutions be real, or in a given interval, and the computation returns a complex number or a number outside the given interval. Exponent overflow/underflow, division by zero, or other domain errors such as $\arcsin (x)$ where |x| > 1are also symptoms of the same problem.

(c)

convergence to a non-root. This is the case where the iterator mistakenly converges to a value which is not a root. A good example is the case of 1/x for bisection search starting with a positive and a negative value.

(d)

hopelessly slow convergence. The convergence achieved by an iterator showing linear convergence with a constant very close to 1. Alternatively, showing just linear convergence in a range which is too large. A simple example is using Newton-Raphson on x¹⁰³=0. For another example, the behaviour shown by 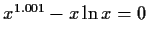$x^{1.001}-x \ln x =0$ with starting values x=10 and x=10⁵⁰⁰⁰ (the solution is $x=0.7941... \times 10^{3960}$). This problem requires 16609 bisection steps to find the first significant digit of the answer.

(e)

pseudo-stable oscillation. The iterator gives values belonging to two or more sets in a cyclic sequence. For example, |x|+10-20e^-x2 has two zeros at 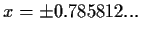$x = \pm 0.785812...$, but if Newton's method is used, and the iteration is started on an |x| > 1.911, the iteration will eventually alternate steadily between +10 and -10.

(f)

incomplete multiple solution. This is a situation where there are many roots, but the rootfinder finds only one of them, or only a few. Most algorithms involve a process where roots are eliminated by algebraic deflation. This leads to an N² algorithm as the expression to zero becomes more complicated. For example, 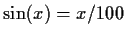$\sin(x) = x/100$ has 63 roots on the real axis.