

Next: Starting values.
Up: Introduction
Previous: Convergence, divergence, random walk,
Usually, advances in most disciplines happen whenever
we are confronted with new problems which are not
solved by the old theories.
In this vein, we present four examples which present serious problems to all
systems, in particular to the existing algorithms
used in Maple's fsolve[2] function.
- (1)
-
for positive x, this equation has two solutions, one small, the
other one huge in magnitude.
The problem here is to find the large positive root, which was the
one wanted by the user who proposed the problem.
The large magnitude of the root will make all methods based on
classical iterations too slow to converge.
- (2)
-
This problem and the next were proposed by Kahan[8].
For positive x, this equation has one solution,
x=0.9999060124....
This value is too close to 1, the limit where the
function can be evaluated without going into the complex plane.
Many algorithms are likely to overshoot (any algorithm
based on the derivative or on estimating the derivative is a
candidate to overshoot) and will try a value outside the valid range.
In this case, the computation is likely to be aborted.
To hit the area of convergence without going into values
greater than 1 for Newton's method, we would have to start in the range
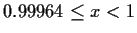 .
This means that an equally spaced grid with at least 2800
values would have to be used.
.
This means that an equally spaced grid with at least 2800
values would have to be used.
- (3)
-
For positive x, this equation has two roots very close to
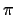 ,
x=3.1415923... and
x=3.1415930....
The difference between each root and
,
x=3.1415923... and
x=3.1415930....
The difference between each root and 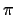 is about
is about
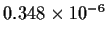 .
The convergence interval for such roots is extremely narrow, and
most methods, even when started close to the roots, will
diverge away from them.
If we would use Newton's iteration, it would converge only if the
initial x is within
.
The convergence interval for such roots is extremely narrow, and
most methods, even when started close to the roots, will
diverge away from them.
If we would use Newton's iteration, it would converge only if the
initial x is within
 from
from 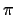 .
If these initial points were sampled from a uniform grid between
0 and 10, we would need more than 3.8 million points.
Graphing software will be often mislead and fail to point these roots.
.
If these initial points were sampled from a uniform grid between
0 and 10, we would need more than 3.8 million points.
Graphing software will be often mislead and fail to point these roots.
- (4)
-
sin(x) = x/100
This equation has 63 real roots in the interval
-96.1 < x < 96.1, and close-call extrema near
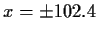 .
The roots come in pairs, each separated by 0.5 to 3.14, closer
as you go away from zero.
Root pairs occur approximately every
.
The roots come in pairs, each separated by 0.5 to 3.14, closer
as you go away from zero.
Root pairs occur approximately every 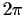 .
In other words, the roots are systematically spaced; the problem
is their multitide.
Any good iterator will easily converge to any root given a
suitable starting guess.
The trick is to find all the roots in a systematic way.
.
In other words, the roots are systematically spaced; the problem
is their multitide.
Any good iterator will easily converge to any root given a
suitable starting guess.
The trick is to find all the roots in a systematic way.


Next: Starting values.
Up: Introduction
Previous: Convergence, divergence, random walk,
Gaston Gonnet
1998-07-08