General fixed point iterations.

An iterator of the form x_i+1 = F(x_i) is called a fixed point iterator. The solution of the equation is the fixed point of F. The conditions for convergence are quite straightforward, since a root $\alpha$ of the equation implies $f(\alpha)=0$, and $\alpha = F(\alpha)$, then

$$x_{i+1}-\alpha = \varepsilon_{i+1} = F(x_i)-F(\alpha) = F'(\xi) \varepsilon_i$$

when $\xi$ is in the interval $(x_i,\alpha)$. So for x where |F'(x)| < 1 we have convergence to a root of f(x). Iterators with order of convergence $\gamma$ satisfy the following asymptotic equation on their errors

$$\varepsilon_{i+1} = O( \varepsilon_i^{\gamma} )$$

and as a natural consequence, $F'(\alpha) = ... = F^{\gamma-1}(\alpha) = 0$ for integer $\gamma$.

Let $\char93 _x(f)$ be the number of occurrences of the variable xin the algebraic expression for f(x). We will not take into account simplification for the time being, we will just consider the number of occurrences as they appear in the expression as it is written. E.g. $\char93 _x( x (\sin x - 1) ) = 2$, whereas $\char93 _x( x \sin x - x ) = 3$Of course, any equation for which $\char93 _x(f)=1$ is trivial to solve by algebraic isolation, if we know the inverses of all the functions used, even if there are multivalue issues. The cases where $\char93 _x(f)=1$ are considered trivial and we will now study the case of $\char93 _x(f) > 1$ exclusively.

It is easy to see, that if $\char93 _x(f)=k$, then by algebraic isolation of each of the occurrences of x we can usually compute kiterators of the form x = F(x) derived from f(x)=0. Except for multivalued functions or principal values, all of these iterators will have the same solution set as the original¹. At this point we will not perform any simplification or any additional manipulation to obtain the iterators. For each occurrence of x we simply isolate it. For example, from $x^{1.001}-x \ln x =0$ we obtain 3 iterators, namely

$$\begin{eqnarray*}x^{1.001} - x \ln x = 0 & \Longrightarrow & x = \left ( x \ln x... ... x^{1.001} } {\ln x} \\ & \Longrightarrow & x = e^{x^{1.001}/x} \end{eqnarray*}$$

and we intentionally did not simplify any of the resulting iterators. As we will see in the next section, it is, in general, possible to obtain more iterators from one equation.

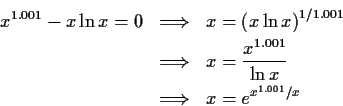
We are now ready to describe the heuristic algorithm. For f(x)=0 we compute all the iterators generated by isolation, F₁(x), F₂(x), ..., F_k(x). For each initial value x₀ we try all the iterators a limited number of times. This is done according to the following procedure

  for x[0] in set_of_initial_values do
      for m = 1 to k do
          for i = 1 to maximum_iterations do
              x[i] := F[m](x[i-1]);
              if computation_failed or outside_domain(x[i])
                   then next m
              else if convergence_achieved
                   then return x[i] 
              else if i>3 and diverging
                   then break
              else if acceleration_possible
                   then x[i] := acceleration(x[i],x[i-1],...)
              end if
          end for i
      end for m
  end for set_of_initial_values;

The idea behind this heuristic is that while it is extremely improbable that all of the iterators will converge, it is also improbable that all of them will fail to converge. By keeping the cost of running each one low, we can try all of them, expecting at least one to succeed. In practice, this heuristic is highly successful even for contrived, ill-behaved examples.