Evaluation by simulation.

``When you can measure what you are speaking about and express it in numbers you know something about it, but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind.'' Lord Kelvin, 1883.

In this vein, we have attempted to measure the behaviour of the iterators by simulation. We randomly generate equations to be solved. This is done top down, generating for each node of the expression tree a random operator. The number of occurrences of x is kept between 2 and 10, various functions are given different probabilities, the equation is forced to be a sum of various terms at the top level and polynomials are discarded. The following are 3 examples of such equations

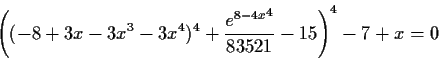
$$x-3+\cosh^{-1}(-3-7x-3x^2) = 0$$

$$\left ( (-8+3x-3x^3-3x^4)^4+\frac{{e^{8-4x}}^4}{83521}-15 \right )^4-7+x = 0$$

$$x+1+10x^2+(-11)^{(11+5/2x)}+\frac{8}{7x(5-\ln(x-7)/9)} = 0$$

Within the limits of the biases (unknown to us) that this random set of equations may impose, we evaluate the iterators by running and measuring them against these equations.

 

Table 1: Simple iterators generated by isolating an x to the lhs of the equation

66644 random equations producing 162314 iterators
method		failures
converged to a root	69.50%	converged to a non-root	3.08%
failed	30.50%	diverged	31.85%
average time	2.639	outside domain	43.44%
time per root	3.797	too many iterations	9.59%
		iterator fails	.01%
iterators per equation	2.436	no iterators	12.03%

For the simple iterators (not included in the groups in the next section) table 1 shows the results of extensive simulations. It is quite remarkable that about 70% of the equations are solved. This compares extremely favourably to the results for Newton's method shown in table 7.