


Next: How general are these
Up: Dayhoff Scores and Evolutionary
Previous: Scores are inconsistent to
As it turns out to be, this is straightforward. For any
scoring matrix E for which SE(d) is strictly monotonic we can invert
SE(d). Our new score is computed using the inverse, i.e.
where w is the actual score obtained from a pair
of aligned sequences
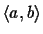 .
.
 |
(7) |
For n sufficiently large, w/n converges to its expected
value SE(d) and d* converges to d. Since SE(d) is a sum
of exponentials in d, it is generally not possible to invert it
algebraically. The computation of the inverse will be done
numerically.
Let
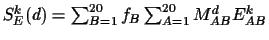 be the kth moment of the scoring matrix E.
The central moments of w/n are:
be the kth moment of the scoring matrix E.
The central moments of w/n are:
E[w/n] = SE(d)
![\begin{displaymath}
\sigma^2(w/n) = E[(w/n - S_E(d))^2] =
\frac{S_E^2(d) - S_E(d)^2}{n} = \frac{\mu_2}{n} \end{displaymath}](img29.gif) |
(8) |
![\begin{displaymath}
E[(w/n - S_E(d))^3] =
\frac{S_E^3(d) - 3S_E^2(d) S_E(d)
+ 2 S_E(d)^3}{n^2} = \frac{\mu_3}{n^2} \end{displaymath}](img30.gif) |
(9) |
![\begin{displaymath}
E[(w/n - S_E(d))^k] =
O(n^{\lfloor -k/2 \rfloor }), \;\;\;\; (k \ge 1) \end{displaymath}](img31.gif) |
(10) |



Next: How general are these
Up: Dayhoff Scores and Evolutionary
Previous: Scores are inconsistent to
Chantal Korostensky
1999-07-14
