Proof 2.1
To prove this, we construct a tree with four leaves, where two
edges are very long and the other edges are very short (see Figure
4 on top). We choose the length of the middle
edge
e to be close to zero. We also choose the distances so that
dAB +
dCD =
dAC +
dBD. For simplicity we look at
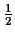
of the distances and scores. As you can see in
Figure
4, both sums of distances are the same:
(
dAB +
dCD)/2 = 70, and
(
dAC +
dBD)/2 = 70.
The scores can be read from the graph. The score
(
dAC +
dBD)/2 is the midpoint of the line between
SAC and
SBD. The intersection with the y axis gives us the score,
which is about 6.3. We do the same for
(
SAB +
SCD)/2. This
case is simpler, as both values are the same, so we already have
the midpoint. The score is around 4.5. If the graph is not a
straight line, there will be points where the sum of the distances
are the same, and sum of the scores are different.
Now we change the length of edge
e slightly by adding a very
small amount.
(
dAC +
dBD)/2 is now slightly greater than
70, but the score
(
SAC +
SBD)/2 is still clearly larger
than the score
(
SAB +
SCD)/2. Even though
dAB +
dCD <
dAC +
dBD, the condition for the scores,
SAB +
SCD
>
SAC +
SBD, does not hold. If the curvature was negative,
then we would move
(
dAC +
dBD)/2 to be slightly lower than
70. Unless there is no curvature, i.e.
S(
d) is a straight
line, we can always find a counter example.
