Lemma 2.5 (Maximum Score)
The maximal score
CSmax(
S) is both
an upper bound on the score for the tree and it is also an upper
bound on the score of an MSA for the underlying sequences.
Proof 2.5
We have already shown that
CSmax(
S) is the upper bound for
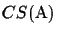
for any
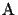
derived from
S.
Since the formula for deriving the score is exactly the same
for both trees and MSAs,
CSmax(
S) also serves as an upper
bound for the score of any tree
T(
S) that can be derived from
S. Therefore, there can be no tree and also no MSA with a higher
score than
CSmax(
S) for a given set of sequences
S.
