Probabilistic Dynamic Programming and Multiple Alignments

The standard DP algorithm for aligning two sequences [15,18,10], requires that we estimate a cost of matching any two individual positions. This is done by the method described in the introduction or by completely empirical cost/similarity functions which assign some value to the alignment of each pair of amino acids. The DP algorithm for aligning sequences can be viewed as an algorithm which takes as parameter such a cost/similarity function,

$$C \;:\; \{\Sigma \cup \phi\} \times \{ \Sigma \cup \phi\} \rightarrow \Re$$

and produces an alignment which maximizes the sum of the Cfunction applied to all aligned pairs¹.

We will use DP over partially built multiple alignments and the C function will be derived from the probability of an EC. We call this aligning algorithm probabilistic dynamic programming.

More precisely, our DP algorithm works over two partial multiple alignments. A partial multiple alignment is a multiple alignment of all the sequences of a subtree of the EPT. Hence a partial multiple alignment is identified by an internal node and a direction in the EPT. E.g. node Y has as descendants the sequence 3 and the node W; node W has sequences 1 and 2 as descendants. The partial multiple alignment for node Y is:

  1     FKQCCWNSLP____RGLSNVALVYQEFMAKCRGESENLQLVTALVINLPSMA
  2   SMFRQCIWNSLS____HGLPETAPIYQPLKARCRGVSENLQLVTEIIINLPTLC
  3   SLWCQCIKASLPLKVIRGTPEVAPLYDQLEQVCRSENQ____VSEIVAKFASLC

For each subtree X and its partial multiple alignment we also compute the T^X and S^X vectors. The C function for this algorithm will be derived from the probability of alignment of two slices of a multiple alignment under the same ancestor. In essence, this is exactly the same idea as in Dayhoff [6], extended so that we can compute the probabilities of alignments not just with two descendant sequences, but with two subtrees of descendants.

The C function is the logarithm of the quotient of probabilities, or

$$C(Y,Z) = 10 \log_{10} \left ( \frac { Pr\{ \mbox{$Y$\space an... ...ce are descendants of $x$ } \} } { Pr\{Y\} Pr \{Z\} } \right )$$

(The factor 10 is retained for purely historical reasons, it was used first by Dayhoff et al. Any constant factor can be used without any material effect.) Using the T and S vectors this becomes

$$C(Y,Z) = 10 \log_{10} \left ( \frac { \sum_x f_x \left ( \sum... ...d_Z} T_z^Z \right ) } { (f \cdot T^Y) (f \cdot T^Z) } \right )$$

$$= 10 \log_{10} \frac{ \sum_x f_x S_x^Y S_x^Z } { (f \cdot T^Y) (f \cdot T^Z) }$$

At this point, we are using DP to align the two subtrees rooted at Y and Z. Hence we still do not have a correspondence between each position of Y and each position of Z. That is why we have to use the sum $\sum_x f_x S_x^Y S_x^Z$ in C. Once that we have found the alignment of Y and Z, then we can compute T^X and S^X for the node we have just joined, the parent of Y and Z.

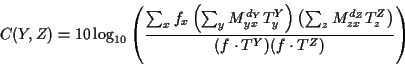
The cost of each computation of C is $O(\vert\Sigma\vert)$ multiplications. The cost of one probabilistic DP alignment is $O(m^2\vert\Sigma\vert)$and the cost of the entire process (including the computation of S and T) is $O(mk\vert\Sigma\vert(\vert\Sigma\vert+m))$.

The alignment at the root of the EPT is the multiple alignment of all the sequences. Notice that for two sequences, this algorithm coincides exactly with DP using Dayhoff matrices, so this presents a continuous generalization of the 2-sequence algorithm.