

Next: Indels.
Up: Probabilistic Dynamic Programming and
Previous: Probabilistic Dynamic Programming and
For any node Y, multiplying SY and TY by an arbitrary
constant k1 has no effect on the dynamic programming algorithm.
(Both SY and TY have to be multiplied by the same constant
so that the equation
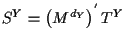 is preserved).
This can be readily verified from the definition of the cost
function for DP, C(Y,X) above.
Similarly, the PAS are not altered by such multiplication,
as the last step normalizes the probabilities to add to 1.
It is then advantageous to normalize the T and S vectors to
prevent underflows which are very likely to occur for large
multiple alignments.
This independence from a constant factor also comes handy for indels.
is preserved).
This can be readily verified from the definition of the cost
function for DP, C(Y,X) above.
Similarly, the PAS are not altered by such multiplication,
as the last step normalizes the probabilities to add to 1.
It is then advantageous to normalize the T and S vectors to
prevent underflows which are very likely to occur for large
multiple alignments.
This independence from a constant factor also comes handy for indels.
Gaston Gonnet
1998-07-14