Phylogenetic tree.

A phylogenetic tree is a representation of evolution. In our case, since we are interested in amino acid sequences, these trees normally describe the evolution of the species where the sequences are found. All the phylogenetic trees are based on a model or theory of evolution. The model of evolution which we consider here is a simple model based on ancestor sequences mutating into descendant sequences where no parallel evolution or horizontal transfers will be considered.

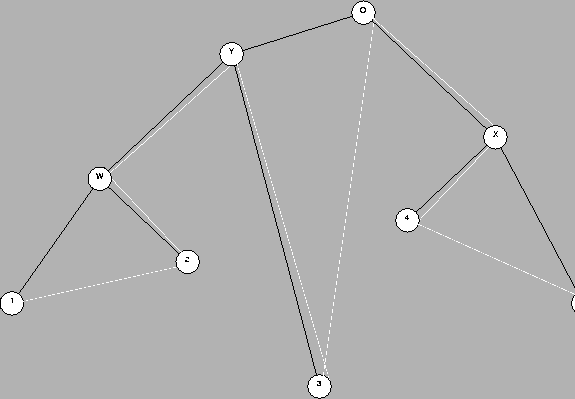
We will assume that we do not have any sequence information corresponding to the internal nodes of the phylogenetic tree. This is the normal situation. All the sequence information is at the leaves. Our phylogenetic trees are always binary (each internal node has degree 3), that is to say, every internal node corresponds to a splitting point in the phylogeny.

In our case, the leaves of the phylogenetic tree are the sequences from present day species. The internal nodes of the tree represent the points of divergence where two different branches of evolution arose. The root of the tree represents the nearest (latest) common ancestor of all the species considered. For example Figure 1

  

Figure 1: Example of an EPT with 5 leaf nodes

is a phylogenetic tree where 1, 2, ..., 5 represent the present-day sequences, W represents the nearest common ancestor of 1 and 2, X is the nearest common ancestor of 4 and 5 and O, the root of the tree, represents the nearest common ancestor of all the sequences.

We are interested in trees with branches which measure amount of evolution in PAM units. We call this an evolutionary phylogenetic tree (EPT). There is no obvious constraint between the distances from the root to the leaves, as it is well known that similar proteins in different species may evolve at different rates.

In Figure 1, if lengths mean amount of evolution, we could say that 3 evolved more from O than 2 and 4. Since we assume that all these descended from a common ancestor, we can also say that 3 evolved more rapidly (mutated more rapidly) than 2 and 4, since in the same amount of time it evolved more.

When the ancestral sequences (O, Y, X and W) are not available for analysis, as it is usually the case, we have to infer their existence and location from the present-day sequences 1, 2, ..., 5. Phylogenetic trees derived only from the information on the leaves are normally called dendrograms.

The evolution from O to Ywill be modelled by a mutation matrix M^d_Y, where d_Y is the PAM distance between O and Y; the evolution from O to 1 by M^d_O1 = M^d_Y+d_W+d₁, etc. The exponent d_ij denotes the distance between node i and node j. d_i (with a single index) denotes the distance between node i and its parent.