Next: Bibliography
Up: Near Optimal Multiple Sequence
Previous: Step 4
We continue this process until all n sequences are in the MSA.
We have shown that the partial score of the MSA is optimal. The
score
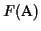 differs from the partial score only in the last
term in the sum. The last term comes from scoring the last
sequence an with the first sequence a1 in the MSA. The
problem is that in the algorithm we never aligned sn with s1
to obtain an optimal pairwise alignment, hence this score may not be
optimal.
differs from the partial score only in the last
term in the sum. The last term comes from scoring the last
sequence an with the first sequence a1 in the MSA. The
problem is that in the algorithm we never aligned sn with s1
to obtain an optimal pairwise alignment, hence this score may not be
optimal.
Figure 10:
The alignment between sequences a1
and an might not be optimal
 |
Lower bound Our algorithm guarantees a lower bound
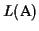 of least
of least
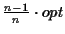 (where opt is the
maximum possible score):
(where opt is the
maximum possible score):
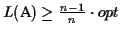 The reason why we choose a place to cut the circle where the
sequences are distant is the following: the score of the pairwise
alignment that has the smallest score (in
The reason why we choose a place to cut the circle where the
sequences are distant is the following: the score of the pairwise
alignment that has the smallest score (in
 )
adds the
smallest amount to the overall sum. Since this is the only
pairwise alignment that is not optimal within the MSA, we get the
greatest possible lower bound
)
adds the
smallest amount to the overall sum. Since this is the only
pairwise alignment that is not optimal within the MSA, we get the
greatest possible lower bound
 .
Hence the lower bound
is
.
Hence the lower bound
is
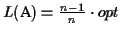 when all the pairwise
scores are the same, and it is greater otherwise.
Our algorithm so far had to invest O(n k2) time for the circular
alignment (where k is the length of the longest sequence) and
O(n2 k2) time to compute all pairwise alignments at the
beginning, which is the most expensive part. Of course the TSP is
exponential in n, but in real cases the calculation of the TSP
order takes only a fraction of the computation time compared to
the time it takes to construct the score matrix of the
when all the pairwise
scores are the same, and it is greater otherwise.
Our algorithm so far had to invest O(n k2) time for the circular
alignment (where k is the length of the longest sequence) and
O(n2 k2) time to compute all pairwise alignments at the
beginning, which is the most expensive part. Of course the TSP is
exponential in n, but in real cases the calculation of the TSP
order takes only a fraction of the computation time compared to
the time it takes to construct the score matrix of the
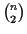 pairwise alignments.
Further improvements At this point we could
consider the following possibilities:
pairwise alignments.
Further improvements At this point we could
consider the following possibilities:
- Do nothing: in most cases the score
is close enough to the optimal that we do not need to make any
adjustments.
- Use a heuristic that shifts
the gap blocks around to come closer to the optimum.
- Use an exhaustive algorithm to shift gap blocks around.
If we want to optimize this alignment the first thing we consider
is: whatever we change, the score between the first n-1
alignments within the MSA can only get worse, since they are
optimal. The only possible improvement would be to increase the score of
the last alignment more than to decrease the scores of all the
other alignments. This makes the search for an optimal alignment
simple: we only have to consider alignments in the search where
the last pairwise alignment n increases, and discard all other
cases.
We show that it is very unlikely that we have to insert a gap
anywhere in order to improve the alignment. Since all the pairwise
alignments within the MSA are optimal except for the alignment of
the last with the first sequence, any gaps we insert will decrease
the score. So the only possible place where we could insert a gap
in order to increase the score is either in sequence a1 or
an (and not both, as this would not affect the alignment
 ):
):
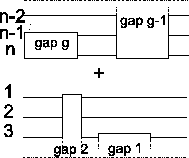
Figure 11:
Insertion of gap g in sequence
a1 or an results in an insertion of gaps in all other
sequences. The score of the MSA is affected at four places
(clouds)
 |
But if we insert a gap g in either sequence an or a1, we
have to insert another gap g' in all other sequences,
otherwise some sequences in the MSA would be longer than
others (see Figure 11). The score of the
previously optimal alignment
 is now
lower by the cost of two gaps (see Figure 11).
In addition, the alignment
is now
lower by the cost of two gaps (see Figure 11).
In addition, the alignment
 has two
additional gaps. Hence the score of the MSA could only improve, if
the alignment
has two
additional gaps. Hence the score of the MSA could only improve, if
the alignment
 has now a score that is
at least four times a gap cost greater than it was before.
Note that the gap cost is usually very low compared to the score
of aligning two amino acids. In our case the fixed gaps cost is
around -14, and the score of aligning two Ala is 2.4
(depending on the PAM distance)
[6,10]. So it is very unlikely that the
alignment
has now a score that is
at least four times a gap cost greater than it was before.
Note that the gap cost is usually very low compared to the score
of aligning two amino acids. In our case the fixed gaps cost is
around -14, and the score of aligning two Ala is 2.4
(depending on the PAM distance)
[6,10]. So it is very unlikely that the
alignment
 gets better after inserting
two gaps. In addition, this situation is very easy to check: we
simply subtract the score of the alignment
gets better after inserting
two gaps. In addition, this situation is very easy to check: we
simply subtract the score of the alignment
 from the optimal score
OPA(s1, sn). If the difference is
smaller than the cost of four gaps, we know for sure that we do
not have to insert a gap - otherwise the alignment
from the optimal score
OPA(s1, sn). If the difference is
smaller than the cost of four gaps, we know for sure that we do
not have to insert a gap - otherwise the alignment
 could not improve by four gaps.
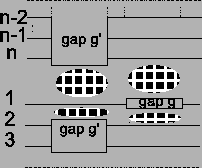
Optimizing the border blocks First we need to
consider where the score changes when gap blocks are moved. Let us
look at the gap block with the label gap g as an example in
Figure 12. If we move this gap block to the
right, the score of the overall alignment is affected at exactly
two places: the score between the pairwise alignment
could not improve by four gaps.
Optimizing the border blocks First we need to
consider where the score changes when gap blocks are moved. Let us
look at the gap block with the label gap g as an example in
Figure 12. If we move this gap block to the
right, the score of the overall alignment is affected at exactly
two places: the score between the pairwise alignment
 changes, and the score on the other side
of the gap block of the alignment
changes, and the score on the other side
of the gap block of the alignment
 changes. The rest of the alignment is not disturbed. This also
means that the gap blocks do not influence each other, unless
they end at the same place.
changes. The rest of the alignment is not disturbed. This also
means that the gap blocks do not influence each other, unless
they end at the same place.
Figure 12:
The movement of a gap block only
affects two places in the alignment.
 |
We call gap blocks that end in either sequence a1 or an
border blocks.
The only way to improve the last pairwise alignment is to
move border blocks around. But whenever we move a gap block, we
also disturb one optimal alignment somewhere between sequences
a1 and an where the border block ends. But it is possible
that moving gap border blocks around will increase the score of
the last alignment more than it will decrease the overall score of
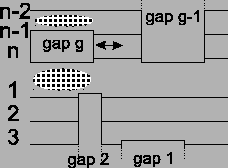
the alignment. The most promising optimization to do would be to
remove a border block by joining border blocks that are cut apart
like the ones in Figure 13. This way we
remove two times the cost of a gap for each border block, and at
the same time the optimal alignments of the neighboring sequences
are only disturbed at one place per block (see Figure
13). To do this we only consider border blocks of
same size, because if we take border blocks of different size,
there would still be a gap left.
Figure 13:
Before the optimization there are four
border blocks. After shifting, two optimal alignments are
disturbed a bit, but in exchange two gap blocks are gone.
 |
If there are several bordering gap blocks of same size we need to
invest some brute force searching, which is exponential in the
number of bordering gap blocks: if there are b bordering gap
blocks it would take in the order of O(kb) time to compute all
possibilities.
However, in real cases, it does not make sense to move one gap
block from one end to the complete other end of the alignment, if
we assume that most gap blocks are more or less placed correctly
within a certain distance. So using heuristics this complexity can
further be reduced. But even without the above optimization we
already have an MSA close to the optimum.
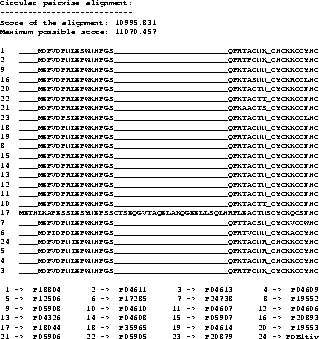
Example To show a real example we took the tat protein
from several strains of the Human Immunodeficiency Virus type 1
(HIV-1). The first alignment was calculated using Clustal W
[35], the second one using our new algorithm,
including shifting of the border blocks. Due to the size of the
MSAs, only a part is shown where the results obtained by the two
methods differ.
The scores are determined using the CS measure. The maximum
possible score in the example is the score determined using the CS
measure but using the OPAs: it is the sum of the OPAs in circular
order (the upper bound for the MSA A, see [11]).
The score obtained with the new algorithm is slightly
better than the score obtained from Clustal W. It is clearly
better at the beginning (if you ask an expert biologist), because
the alignment has only one big gap whereas the alignment obtained
from Clustal W has two gaps.
With the above example we do not want to
prove that our method performs generally better than Clustal W,
but we want to show that our method is usable and produces good
results.
Discussion Our algorithm produces an MSA that has a
score of at least
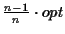 ,
where opt is the
maximum possible score. It takes in the order
O(n2 k2) time
given a circular tour. The calculation of such a tour using a TSP
algorithm can be done very efficiently, and in realistic cases the
calculation time of a TSP cycle can be ignored. The alignment can
then further be improved using an exact or heuristic algorithm. A
further advantage of this algorithm is that it does not need to
calculate an evolutionary tree but uses a scoring function that
takes such a tree into account.
Acknowledgements We would like to thank Todd Wareham for
various references and Ulrike Stege for reading the paper.
,
where opt is the
maximum possible score. It takes in the order
O(n2 k2) time
given a circular tour. The calculation of such a tour using a TSP
algorithm can be done very efficiently, and in realistic cases the
calculation time of a TSP cycle can be ignored. The alignment can
then further be improved using an exact or heuristic algorithm. A
further advantage of this algorithm is that it does not need to
calculate an evolutionary tree but uses a scoring function that
takes such a tree into account.
Acknowledgements We would like to thank Todd Wareham for
various references and Ulrike Stege for reading the paper.



Next: Bibliography
Up: Near Optimal Multiple Sequence
Previous: Step 4
Chantal Korostensky
1999-07-14