- Schreiben Sie eine Funktion, die die ersten
 Tschebyscheff-Polynome an den Stützstellen gegeben durch den Vektor
Tschebyscheff-Polynome an den Stützstellen gegeben durch den Vektor
 auswertet, siehe Seite
auswertet, siehe Seite ![[*]](crossref.png) .
Die erste Zeile des Funktionenfiles soll die Form
.
Die erste Zeile des Funktionenfiles soll die Form
function T = tscheby(x,n)
haben.
- Wurzelberechnung. Das Newton-Verfahren zur Berechnung der
Wurzel einer positiven Zahl
 ist gegeben durch
ist gegeben durch
Schreiben Sie eine eigene Funktion
[x, iter] = wurzel(a, tau),
die  auf eine gewisse Genauigkeit
auf eine gewisse Genauigkeit  berechnet:
berechnet:
Wenn nur ein Eingabeparameter vorgegeben wird, so soll
 gesetzt werden.
gesetzt werden.
Sehen Sie auch einen Notausgang vor, wenn Folge  nicht
(genügend schnell) konvergiert.
nicht
(genügend schnell) konvergiert.
- Lösen Sie die gewöhnliche Differentialgleichung
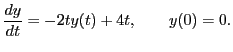 |
(5.1) |
Die analytische Lösung ist
Wir wollen die Funktion ode23 zur Lösung dieser
Differentialgleichung verwenden. ode23 geht von einer
Differentialgleichung der Form
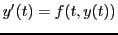
plus Anfangsbedingungen

aus. Deshalb schreiben Sie zunächst eine Funktion, z.B.
fun_ex1.m, die zwei Eingabeargumente,  und
und 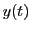 ,
und ein Ausgabeargument,
,
und ein Ausgabeargument,  , hat. Danach lösen Sie die
Gleichung (5.1) im Interval
, hat. Danach lösen Sie die
Gleichung (5.1) im Interval ![$ [0,3]$](img192.png) . ode23 hat
zwei Ausgabeparameter, Vektoren (t, y) der selben
Länge, die die (approximativen) Werte der Lösung
. ode23 hat
zwei Ausgabeparameter, Vektoren (t, y) der selben
Länge, die die (approximativen) Werte der Lösung 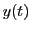 and gewissen
Stellen
and gewissen
Stellen  enthält. Die Lösung kann so leicht geplottet werden.
enthält. Die Lösung kann so leicht geplottet werden.
- Räuber-Beute-Modell. Im Räuber-Beute-Modell von
Lotka-Volterra geht man von zwei Populationen aus, einer
Beutepopulation
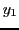 und einer Räuberpopulation
und einer Räuberpopulation 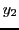 . Wenn ein
Räuber ein Beutetier trifft frisst er es mit einer bestimmten
Wahrscheinlichkeit
. Wenn ein
Räuber ein Beutetier trifft frisst er es mit einer bestimmten
Wahrscheinlichkeit 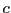 . Wenn die Beutepopulation sich alleine
überlassen wird, so wächst sie mit einer Rate
. Wenn die Beutepopulation sich alleine
überlassen wird, so wächst sie mit einer Rate  . (Das
Nahrungsangebot ist unendlich gross.) Die Räuber haben als einzige
Nahrung die Beutetiere. Wenn diese nicht mehr vorhanden sind, so
sterben auch die Räuber (mit einer Rate
. (Das
Nahrungsangebot ist unendlich gross.) Die Räuber haben als einzige
Nahrung die Beutetiere. Wenn diese nicht mehr vorhanden sind, so
sterben auch die Räuber (mit einer Rate  ) aus.
) aus.
Hier betrachten wir das Beispiel von Hasen und Füchsen, deren
Bestände durch  und
und  bezeichnet seien. Das
Räuber-Beute-Modell von Lotka-Voltarra hat die Form
bezeichnet seien. Das
Räuber-Beute-Modell von Lotka-Voltarra hat die Form
Alle Koeffizienten  ,
,  ,
, 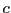 und
und 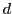 sind positiv. Man rechen das
Modell mit folgenden Parametern durch:
sind positiv. Man rechen das
Modell mit folgenden Parametern durch:
- Zuwachsrate Hasen:
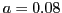 ,
,
- Sterberate Füchse:
 ,
,
- Wahrscheinlichkeit, bei Treffen gefressen zu werden:
 ,
,
- Beutewahrscheinlichkeit der Füchse:
 ,
,
- Anfangsbedingungen: Anfangsbestand Hasen 500, Anfangsbestand
Füchse 20.
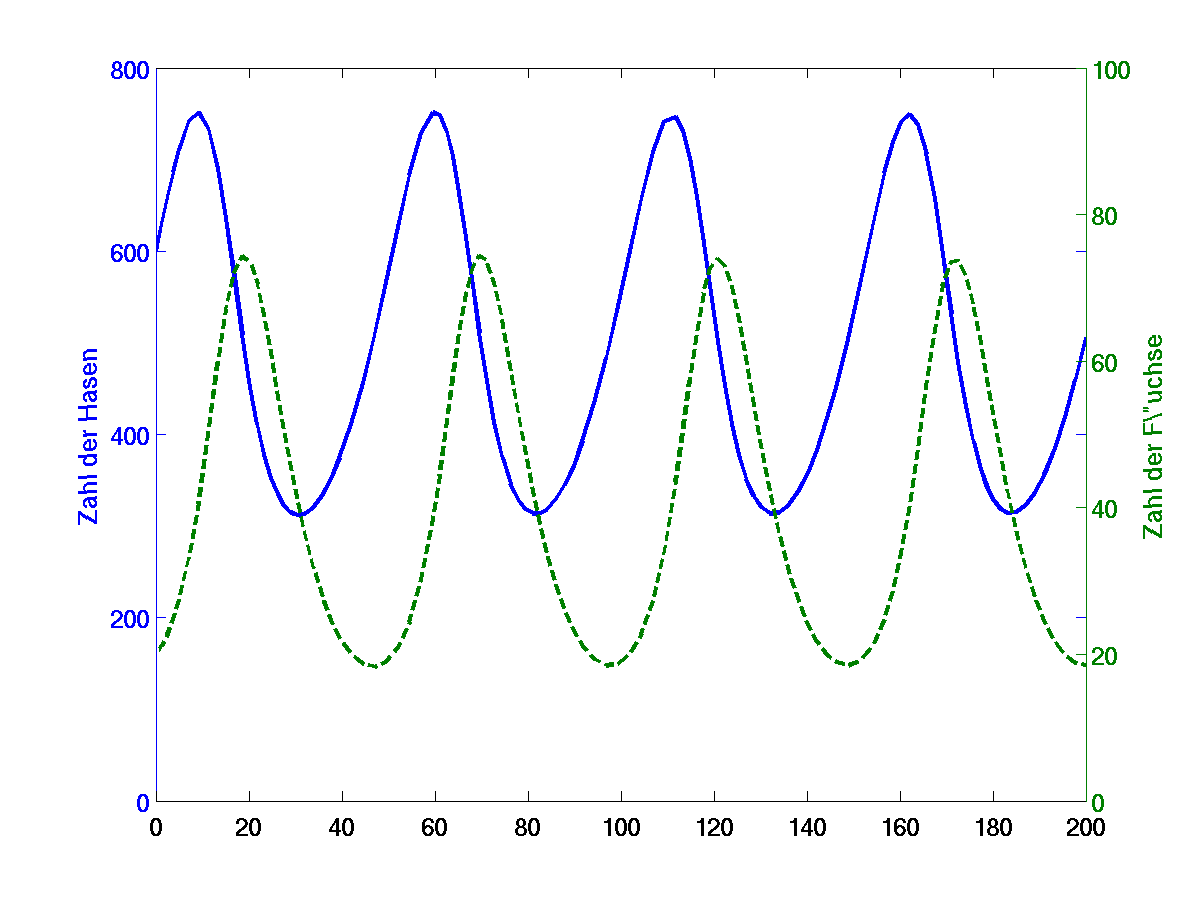
Die Simulation ergibt eine periodische Schwingung, wobei die Maxima
der Räubertiere jeweils eine kurze Weile nach den Maxima der
Beutetiere auftreten.
Abbildung 5.2:
Simulation eines Räuber-Beute-Modell
|
 |
Verwenden Sie ode34 und lösen Sie die Differentialgleichung
im Interval ![$ [0,200]$](img205.png) . Das M-File, das Sie schreiben müssen, sieht
wie in der vorigen Aufgabe aus, hat aber einen 2-komponentigen Vektor
als Ausgabeargument. Zur Darstellung der beiden Lösungskomponenten
können Sie den Befehl plotyy verwenden, vgl. Abschnitt 7.4.
. Das M-File, das Sie schreiben müssen, sieht
wie in der vorigen Aufgabe aus, hat aber einen 2-komponentigen Vektor
als Ausgabeargument. Zur Darstellung der beiden Lösungskomponenten
können Sie den Befehl plotyy verwenden, vgl. Abschnitt 7.4.
- Die nicht-lineare gewöhnliche Differentialgleichung dritter
Ordnung
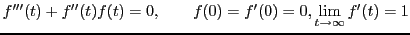 |
(5.3) |
hat keine analytische Lösung. Da MATLABs ODE-Löser Anfangswertprobleme
erster Ordnung lösen, müssen wir zunächst (5.3) in ein
solches umschreiben. Wir setzen
Somit erhält die ursprüngliche gewöhnliche Differentialgleichung
dritter Ordnung die Form
Die Anfangsbedingungen für 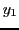 und
und 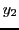 sind bekannt:
sind bekannt:
 und
und
 . Wir haben keine Anfangsbedingung für
. Wir haben keine Anfangsbedingung für 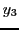 . Wir
wissen aber, dass
. Wir
wissen aber, dass  mit
mit
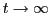 gegen 1
konvergiert. Deshalb kann die Anfangsbedingung für
gegen 1
konvergiert. Deshalb kann die Anfangsbedingung für 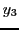 verwendet
werden, um
verwendet
werden, um
 zu erhalten. Durch versuchen erhält man
zu erhalten. Durch versuchen erhält man
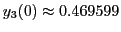 . Die Lösung sieht wie in
Abb. 5.3 aus.
. Die Lösung sieht wie in
Abb. 5.3 aus.
Abbildung 5.3:
ODE dritter Ordnung
|
 |
- Versuchen Sie die Konstante in der Anfangsbedingung für
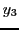 zu
bestimmen. Man muss dabei nicht bis
zu
bestimmen. Man muss dabei nicht bis  gehen;
gehen; 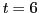 reicht.
Versuchen Sie also mit fzero eine Nullstelle der Funktion
reicht.
Versuchen Sie also mit fzero eine Nullstelle der Funktion
zu berechnen. Hier bedeutet  der Funktionswert von
der Funktionswert von 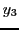 an
der Stelle
an
der Stelle 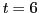 wenn die Anfangsbedingung
wenn die Anfangsbedingung
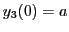 gewählt
wurde.
gewählt
wurde.
![[*]](crossref.png) .
Die erste Zeile des Funktionenfiles soll die Form
.
Die erste Zeile des Funktionenfiles soll die Form
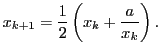
![]() auf eine gewisse Genauigkeit
auf eine gewisse Genauigkeit ![]() berechnet:
berechnet:
![]() nicht
(genügend schnell) konvergiert.
nicht
(genügend schnell) konvergiert.
![]() und
und ![]() bezeichnet seien. Das
Räuber-Beute-Modell von Lotka-Voltarra hat die Form
bezeichnet seien. Das
Räuber-Beute-Modell von Lotka-Voltarra hat die Form
![]() . Das M-File, das Sie schreiben müssen, sieht
wie in der vorigen Aufgabe aus, hat aber einen 2-komponentigen Vektor
als Ausgabeargument. Zur Darstellung der beiden Lösungskomponenten
können Sie den Befehl plotyy verwenden, vgl. Abschnitt 7.4.
. Das M-File, das Sie schreiben müssen, sieht
wie in der vorigen Aufgabe aus, hat aber einen 2-komponentigen Vektor
als Ausgabeargument. Zur Darstellung der beiden Lösungskomponenten
können Sie den Befehl plotyy verwenden, vgl. Abschnitt 7.4.


