Nächste Seite: 8.2 Singulärwertzerlegung Aufwärts: 8. Anwendungen aus der Vorherige Seite: 8. Anwendungen aus der Inhalt
Gegeben sind die Punkte
Gesucht ist ein Kreis, der ``möglichst gut'' durch die Punkte
verläuft.
Die Gleichung für Kreis mit Mittelpunkt ![]() und Radius
und Radius ![]() lautet
lautet
Bei Rundheitsmessungen in der Qualitätskontrolle ist es erwünscht,
dass die Abstände ![]() der gemessenen Punkte zum ausgeglichenen
Kreis minimiert werden. Sei
der gemessenen Punkte zum ausgeglichenen
Kreis minimiert werden. Sei
Dann soll nach dem Gauss-Prinzip
![]() so bestimmt werden, dass
so bestimmt werden, dass
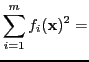 minimal
minimal
Dieses nichtlineare Ausgleichsproblem kann nach dem
Gauss-Newton Verfahren gelöst werden: Sei
![]() eine
Näherungslösung. Man entwickelt
eine
Näherungslösung. Man entwickelt
 |
||
 |
% Kreisanpassung nach der Methode der kleinsten Quadrate
% unter Verwendung des Gauss-Newton Verfahrens
% (zeigt auch einige Moeglichkeiten von MATLAB)
%
xi = [ 0.7 3.3 5.6 7.5 6.4 4.4 0.3 -1.1]'; % Gegebene
% Messpunkte
eta = [ 4.0 4.7 4.0 1.3 -1.1 -3.0 -2.5 1.3]';
%
[xi, eta]
xmin = min(xi); xmax = max(xi); ymin = min(eta); ymax = max(eta);
dx = (xmax - xmin)/10; dy = (ymax -ymin)/10;
axis([xmin-dx xmax+dx ymin-dy ymax+dy]);
axis('equal'); % damit Einheiten auf beiden Achsen etwa
% gleich sind
hold; % nachfolgende Plots im gleichen
% Koordinatensystem
plot(xi,eta,'o'); pause; % Es geht weiter mit RETURN
phi = [0:0.02:2*pi]; % um den Naeherungskreis zu zeichnen
h = size(xi); n = h(1); % Bestimmung der Anzahl Messwerte
x = [0.1 1 1]'; % Startwerte : m1 = x(1), m2 = x(2), r =
% x(3)
%
text(0.6,0.9, 'm1 =','sc'); % Ueberschrift
text(0.71,0.9,'m2 =','sc');
text(0.82,0.9,'r =','sc'); i = 0.9;
format long; minimum = []; % soll norm(f) fuer jede Iteration
% speichern
while norm(h)>norm(x)*1e-4, % solange Korrektur h gross ist ...
u = x(1) + x(3)*cos(phi); % zeichne Naeherungskreis
v = x(2) + x(3)*sin(phi);
i = i-0.05;
text(0.6,i, num2str(x(1)),'sc');
text(0.71,i, num2str(x(2)),'sc');
text(0.82,i, num2str(x(3)),'sc');
plot(u,v); pause;
a = x(1)-xi; b = x(2)-eta;
fak = sqrt(a.*a + b.*b);
J = [a./fak b./fak -ones(size(a))]; % Jacobimatrix
f = fak -x(3); % rechte Seite
h = -J\f; % Aufloesen nach Korrektur (QR)
x = x + h;
[x h ], pause % Ausdrucken x und Korrektur
minimum = [minimum norm(f)];
end;
minimum'
ans =
0.70000 4.00000 Gegebene Punkte x_i, y_i
3.30000 4.70000
5.60000 4.00000
7.50000 1.30000
6.40000 -1.10000
4.40000 -3.00000
0.30000 -2.50000
-1.10000 1.30000
Bedeutung des Ausdrucks:
ans =
3.09557664665968 2.99557664665968 m_1 dm_1
0.62492278502735 -0.37507721497265 m_2 dm_2
3.57466996351570 2.57466996351570 r dr
ans =
3.04180805000003 -0.05376859665966
0.74825578400634 0.12333299897899
4.10472289255764 0.53005292904193
ans =
3.04326031235803 0.00145226235801
0.74561749573922 -0.00263828826712
4.10585853340459 0.00113564084696
ans =
3.04323750977451 -0.00002280258352
0.74567950486445 0.00006200912523
4.10585580071342 -0.00000273269117
ans =
12.24920034893416 ||r||
1.63800114348265
0.54405321190190
0.54401144797876
Peter Arbenz 2008-09-24