Nächste Seite: 8.3 Gewöhnliche Differentialgleichungen Aufwärts: 8. Anwendungen aus der Vorherige Seite: 8.1 Kreisausgleichsproblem Inhalt
Es ist einfach, neue Funktionen in MATLAB einzuführen. Man muss dazu ein MATLAB Programm schreiben und es als M-File abspeichern.
Funktionen können Inputparameter haben und ein oder mehrere Resultate liefern.
MATLAB Funktionen werden auch als M-Files gespeichert. Im Unterschied zu einem Script-file muss die erste Zeile das Wort function enthalten. Ein Funktionen-File unterscheidet sich von einem Script-File indem Argumente übergeben werden können und indem Variablen, die im File definiert werden, lokal sind. Diese werden also aus dem Arbeitsspeicher entfernt, sobald die Funktion durchlaufen ist. Mit Funktionen-Files kann der Benutzer MATLAB nach seinen Bedürfnissen erweitert.
Wir betrachten zunächst die Wurzelfunktion sqrtm von MATLAB.
Wenn wir als Beispiel die Matrixwurzel aus der Matrix
![$\displaystyle A = \left[
\begin{array}{cc}4 & 9\\ 25 & 36
\end{array}\right]
$](img265.png)
>> A = [4 9; 25 36] >> W = sqrtm(A) W = 0.8757 + 1.2019i 1.3287 - 0.2852i 3.6907 - 0.7922i 5.5998 + 0.1880iDass W wirklich eine Wurzel ist, sieht man beim Quadrieren:
W*W ans = 4.0000 - 0.0000i 9.0000 - 0.0000i 25.0000 + 0.0000i 36.0000 + 0.0000iDie Quadratwurzel einer diagonalisierbaren Matrix kann mittels
function W1 = wurzel(A); % Berechnet die Quadratwurzel von A % Aufruf W1 = wurzel(A) [Q,D] = eig(A); D1 = sqrt(D); W1 = Q*D1/Q;berechnet werden. Werden diese Anweisungen als File mit dem Namen wurzel.m abgespeichert, so kann die Funktion wie eine eingebaute MATLAB Funktion verwendet werden:
>> help wurzel Berechnet die Quadratwurzel von A Aufruf W1 = wurzel(A)Wir sehen, dass die Kommentarzeile nach der ersten Kopfzeilen automatisch von der Help-Funktion ausgedruckt werden. Mittels type wird das File ganz ausgedruckt:
>> type wurzel function W1 = h(A); % Berechnet die Quadratwurzel von A % Aufruf W1 = wurzel(A) [Q,D] = eig(A); D1 = sqrt(D); W1 = Q*D1/Q;und wurzel unterscheidet sich im Gebrauch nicht (wohl aber bezüglich Rundungsfehler) von sqrtm
>> wurzel(A) - sqrtm(A)
ans =
1.0e-15 *
0 - 0.4441i 0.2220 + 0.1110i
0 + 0.2220i 0 - 0.1388i
Funktionen können mehrere Resultate liefern. Als Beispiel betrachten
wir
die Singulärwertzerlegung einer Matrix. Sei ![]() eine
eine
![]() Matrix. Dann existieren eine orthogonale
Matrix. Dann existieren eine orthogonale ![]() Matrix
Matrix ![]() , eine
orthogonale
, eine
orthogonale ![]() Matrix
Matrix ![]() und eine
und eine ![]() Diagonalmatrix
Diagonalmatrix ![]() , so dass
, so dass
>> A =
22 52 1 93 70 33
5 83 38 85 91 63
68 3 7 53 76 76
68 5 42 9 26 99
93 53 69 65 5 37
38 67 59 42 74 25
>> svd(A) % svd, allein aufgerufen, liefert den Vektor der
% singulaeren Werte der Matrix.
ans =
305.3327
121.8348
89.4757
57.6875
37.0986
3.0329
>> [U S V ] = svd(A) % Mit den Parametern U,S,V auf der linken Seite
% wird die vollstaendige Zerlegung berechnet.
% Dabei sind U und V orthogonal und S diagonal.
U =
0.3925 0.4007 -0.1347 -0.5222 -0.1297 -0.6146
0.5068 0.4598 -0.0681 0.3545 -0.4612 0.4345
0.4017 -0.2308 -0.5706 -0.3185 0.4366 0.4096
0.3231 -0.6371 -0.2695 0.3813 -0.3286 -0.4046
0.4050 -0.3802 0.6980 -0.3788 -0.1325 0.2077
0.3992 0.1559 0.3030 0.4597 0.6741 -0.2427
S =
305.3327 0 0 0 0 0
0 121.8348 0 0 0 0
0 0 89.4757 0 0 0
0 0 0 57.6875 0 0
0 0 0 0 37.0986 0
0 0 0 0 0 3.0329
V =
0.3710 -0.6348 0.1789 -0.4023 0.4171 -0.3026
0.3717 0.3728 0.4647 0.2416 -0.1945 -0.6408
0.2867 -0.2260 0.5365 0.4805 0.0601 0.5869
0.4810 0.3301 0.0796 -0.6448 -0.3068 0.3787
0.4719 0.3727 -0.4480 0.2346 0.6149 0.0676
0.4335 -0.3989 -0.5071 0.2794 -0.5589 -0.0733
>> norm(U*S*V'-A) % Kontrolle der Matrixzerlegung
ans =
3.0075e-13
Die Konditionszahl einer Matrix
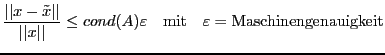
>> cond(A)
ans = 100.6742
>> S(1,1)/S(6,6) % Verhaeltnis der singulaeren Werte = cond(A) !
ans = 100.6742
>> S(6,6) = 0.0003 % Wir verkleinern den kleinsten singulaeren
% Wert, damit machen wir die Kondition schlechter.
S =
305.3327 0 0 0 0 0
0 121.8348 0 0 0 0
0 0 89.4757 0 0 0
0 0 0 57.6875 0 0
0 0 0 0 37.0986 0
0 0 0 0 0 0.0003
> AS = U*S*V' % Neue Matrix
AS =
21.4361 50.8057 2.0938 93.7058 70.1259 32.8633
5.3987 83.8443 37.2268 84.5010 90.9110 63.0966
68.3759 3.7960 6.2710 52.5296 75.9161 76.0911
67.6287 4.2136 42.7202 9.4647 26.0829 98.9100
93.1906 53.4036 68.6304 64.7615 4.9574 37.0462
37.7773 66.5284 59.4319 42.2787 74.0497 24.9460
>> cond(AS)
ans = 1.0178e+06 % Die Kondition der Matrix AS ist viel
% groesser als jene der Matrix A.
>> x = [1:6]/17 % Waehlen einen Loesungsvektor
x =
0.0588 0.1176 0.1765 0.2353 0.2941 0.3529
>> x = x'; b = A*x; bs = AS*x; % Wir berechnen zugehoerige rechte Seiten
>> b' =
61.7059 85.7647 67.2353 56.7059 53.7059 61.0000
>> bs' =
61.8801 85.6416 67.1192 56.8206 53.6470 61.0688
>> xa = A\b % Loesen des Gleichungssystems A*x = b
xa =
0.0588
0.1176
0.1765
0.2353
0.2941
0.3529
>> norm(xa-x)/norm(x)
ans =
7.5815e-15
>> eps % Maschinengenauigkeit. Die Loesung xa ist etwas
eps = % genauer als die Schranke angibt.
2.2204e-16
>> xas= AS\bs % Loesen des Gleichungssystems AS*x = bs
xas =
0.0588
0.1176
0.1765
0.2353
0.2941
0.3529
>> norm(xas-x)/norm(x) % Die Loesung xas ist wie erwartet um
% ca. cond(AS) Stellen falsch.
ans =
2.1368e-11
Peter Arbenz 2008-09-24